流れ 2022年3月号 目次
― 特集テーマ: 流体工学部門講演会 3月号 ―
| リンク一覧にもどる | |
印象派物理学への誘い:流体・界面などの研究から
奥村 剛
お茶の水女子大学
1.はじめに
2021年11月に開催された「第99期流体工学部門講演会」で基調講演の機会をいただいた.オンライン開催であったので,その場で,講演の手ごたえを感じることは難しかった.しかし,講演当日の夜,意外な形で反響を実感することとなった.拙著[1]が,アマゾンの「物理学一般関連書籍」の売れ筋ランキングで10位になっていたのだ.すぐにランキングは正常な(?)順位に戻ったので,これは間違いなくこの講演のインパクトだったと信じている.本稿では,この講演の内容をごく手短にまとめるが,講演では触れなかったエピソードも含める.
2.印象派物理学とは
印象派物理学とは,西洋絵画における「印象派」にちなんだ言葉である.印象派画家たちは,あえて,詳細を描かず,目に見えているものをシンプルに捉えることで,生き生きとした躍動感を導き出し,美の本質をエレガントに描き出す.物理学においても,現象をシンプルに捉えて,そこに潜む物理的本質を描き出すことができる.講演では,いくつもの研究例を通して,このことをお目にかけた.
私が印象派物理学というスタイルに触れたのはde Gennes先生の多くの著作を通してである.私はパリで先生と共同研究する機会を得て(英語概要の文献[1]参照),ますます,このスタイルに憧れた.そして,先生の表面張力に関する著書を訳した際には[2],その「訳者あとがき」を「印象派物理の薦め」というタイトルで書くに至った.
3.研究例:バブルの破裂
我々は,ヘレ・ショウのセルとも呼ばれる平べったい容器を使った界面現象の研究を行ってきている.そもそも私は理論物理学者で物理の実験の研究経験は皆無だった.しかし,印象派物理に魅せられて,学生と実験研究を開始した.de Gennes先生は理論家であったが,周りの実験研究者と非常によくコミュニケーションして,シンプルでエレガントな印象派物理学を展開していたからである.そして,前述の「訳者あとがき」を書いた4年後の2007年に,はじめての実験研究の論文を発表するに至った[3].以来,ヘレ・ショウのセルを使った研究を発表し続けている[4,5].ここでは,その一例を紹介する[6].
この研究[6]の概要を図1に示した.容器に粘度の高い液体を入れ,底から空気を注入することで気液界面にバブルを生成する.バブルを閉じ込めた液体薄膜は重力のために厚みが減少することがわかっている[3]が,やがて,自然に破裂する.本研究では,この薄膜の破裂の速度を,さまざまな条件で直接に測定した.その結果を図2(a)に示す.ここでは,破裂速度Vを厚みhの関数としてあらわしている.セルの厚みDと液体の粘性ηも変化させている(グラフの凡例を参照).なお,図2(a)のデータは,液体の表面張力γは,ほぼ一定の条件下で取得されている.
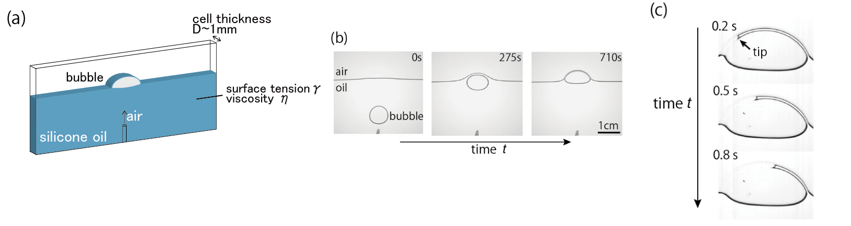
図1:実験の概要.(a)実験装置.(b)バブル上昇の様子.(c)バブルの破裂の様子.文献[6]より転載(CC BY 4.0).
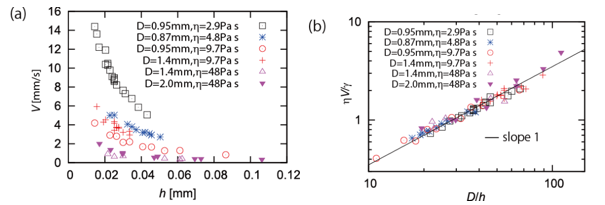
図2:「データコラプス」の一例.(a)生データ.(b)スケーリング則によって軸を取り直したグラフ.文献[6]より転載(CC BY 4.0).
後で少し説明するように,この破裂現象に対して,理論的な考察から,破裂速度Vが次式(1)を満たす可能性を導くことができる.
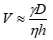 |
(1) |
この式は,二つの変数ηV/γとD/hが比例関係にあることを意味するので,もし,図2(a)のデータがこの理論で記述されているならば,これら二つの変数を軸にとってデータをプロットしなおせば,すべてのデータは一直線上にのるはずである.それが,図2(b)に示されている.このように軸を取り直すことで,すべてのデータがあるマスターカーブに収れんする様子を「データコラプス」と呼ぶ.このようにして実験と理論の一致を明確に示すことは,印象派物理学の常套手段であり,これは後述する「臨界現象の物理学」にルーツを持つ.
ところで,式(1)の右辺は,各パラメータについてべき乗の形をしている.γとDについては1乗,ηとhについては-1乗になっている.このようにある物理量(ここでは速度V)が,パラメータのべき乗で表されたものをスケーリング則と呼ぶ.
印象派物理の特徴の一つは,このようなスケーリング則を見出すことである.もちろん,物理法則はいつもそんなに簡単ではない.しかし,パラメータについて極限的な状況が成立すれば,図2に示したようにスケーリング則を確立することができる.ここでは,粘性が高い極限,hがDに比べて小さい極限,さらにはバブルの半径に対してDが小さい極限,などを仮定すると,式(1)を導くことができる.実は,この実験ではこれらの極限的状況はそれほど良く成り立っているわけではない.ところが,実際には,ある程度極限的な状況に追い込んでやれば,驚くほどよくスケーリング則が成立することがある,というのが我々の実感である.
極限的状況を考えて式を導く際には,式(1)で無視されている数値係数を求めることははじめからあきらめる.この点を,ストークスの抵抗則F=6πηRVを例にして説明する.この法則は、粘性ηの流体中を速度Vで移動する半径Rの固体球に働く抵抗力Fを表すものである.ご存じの方も多いと思うが,この法則に現れる数値係数6πを理論的に導くことはあきらめ,代わりにスケーリング則F≃ηRVを導くことは非常に簡単である.実際,この場合の粘性応力はηV/Rにスケールするはずで,力Fを導くには,この応力に球の面積のスケールであるR2を掛ければよいだけである.スケーリング則である式(1)も,ナビエストークス方程式,あるいは,エネルギーバランスを次元解析することで,似たようにシンプルな考察から導くことができる.
「あきらめる」とはいっても,実験と理論の一致をグラフで示せれば,そのマスターカーブから数値係数も「予言」できてしまう.ただ,我々の考えている状況は,それほど自明なものではない.実際,我々がこのように示した数値係数の予言値が,独立した解析理論や数値シミュレーションによって検証された例は,まだ,ない.近い将来,このような検証研究が現れることを期待したい.
4.おわりに
上に示したバブルの破裂の研究例では,数学的な枝葉末節にあえて目をつぶることで,シンプルで明確な結論を得ることができた.多くの場合には,上に見たようなスケーリング則に着目することになるが,印象派物理学は,これには限定されずに,もっと広い意味で,シンプル&エレガントをめざす研究と解釈してもらいたい[1].一方,スケーリング則に着目し,いろいろな極限を考えることで,ある現象に対して,いくつものスケーリング則を得て,それらがどのようにクロスオーバーするかを調べることで,現象の全貌に迫ることもできる[4,5].
駆け足になるが、最後に、強調したいことを並べる。我々は,このような印象派の精神で,しずくやバブル,粉粒体,天然物質の強靭性などの多くの研究を行ってきている.また,物理学においては,スケーリング則は,歴史的に見て非常に大きな意味を持っており,熱力学相転移における臨界現象との深い結びつきをもつ.さらに,この臨界現象とのあるアナロジーによって,高分子物理学の大問題が解決された歴史がある(de Gennes教授は,これらの業績で1991年にノーベル物理学賞を受賞している).最近,我々は,バブルの引きちぎれの問題で臨界現象とのアナロジーを見出すことに成功してきている.これらに興味のある方は,ぜひ,[1]を参照いただきたい.さらに,最近は,切り紙の伸長の力学と臨界現象のアナロジーについても解明を進めている[7].また、印象派の香りのするフランスの教科書[8,9]も文献リストに加えたので,参考にしていただければ幸いである.
本研究は,JSPS科研費JP19H01859の助成を受けたものである.
5.文献
| [1] | 奥村剛「印象派物理学入門」(日本評論社, 2020). |
| [2] | 奥村剛「表面張力の物理学」(吉岡書店, 2003; CD付第2版 2008). |
| [3] | Ayako ERI and Ko OKUMURA, Lifetime of a two-dimensional air bubble, Phys. Rev. E Rapid Communication 76 (2007) 060601. |
| [4] | Maria YOKOTA and Ko OKUMURA, Dimensional crossover in the coalescence dynamics of viscous drops confined in between two plates, Proc. Nat. Acad. Sci. (USA), 108 (2011) 6395–6398. |
| [5] | Ko Okumura, Viscous dynamics of drops and bubbles in Hele-Shaw cells: drainage, drag friction, coalescence, and bursting, Adv. Colloid Interface Sci. 255, 64-75 (2018) |
| [6] | Mayuko Murano and Ko Okumura, Bursting dynamics of viscous film without circular symmetry: the effect of confinement, Phys. Rev. Fluids 3, 031601(R) (2018). |
| [7] | Midori Isobe and Ko Okumura, Continuity and discontinuity of kirigami’s high-extensibility transition: a statistical-physics viewpoint, Phys. Rev. Research 1, 022001(R)(2019). |
| [8] | 粉粒体:中西 秀,奥村 剛共訳,粉粒体の物理学‐砂と粉と粒子の世界への誘い‐(J. Duran著),310頁,吉岡書店 (2002年). |
| [9] | ムース・フォーム:奥村 剛監訳,梶谷忠志,武居淳,竹内一将,山口哲生 共訳,ムースの物理学:構造とダイナミクス(I. Canta, S. Cohen-Addad, F. Elias, F. Graner, R. Höhler, O. Pitois, F. Rouyer, A. Sant-Jalmes著),336頁,吉岡書店(2016年). |

