流れ　2022年3月号　目次

―　特集テーマ： 流体工学部門講演会　3月号　― 巻頭言 （橋本，松田，朴） 印象派物理学への誘い：流体・界面などの研究から 奥村 剛（お茶の水女子大学） 遠心羽根車の回転円板と静止円板間の隙間流れと摩擦トルクの関係 阪井 健人，稲葉 夢乃，宮川 和芳（早稲田大学），佐野 岳志，前田 聡（三菱重工業株式会社） べき乗則流体の伸長レオロジーとせん断レオロジーの関係 松本 祐月（東京農工大学），田川 義之（東京農工大学） 火炎旋風の魅力 田中　実（明星大学） 　｜　リンク一覧にもどる　｜

 

べき乗則流体の伸長レオロジーとせん断レオロジーの関係

松本 祐月， 田川 義之 （東京農工大学）

　令和3年11月に開催された第99期日本機械学会流体工学部門講演会において，優秀講演表彰を頂いた．本稿ではその発表内容に関連して，塗料の伸長レオロジーとせん断レオロジーの関係について，これまでの研究成果の概要を述べる．

1.　緒　　　言

　従来のスプレー塗装に代わり, 液体ジェットによるオンデマンド型塗装の実用化が進められている⁽¹⁾. オンデマンド型塗装とは, 塗料を必要量・必要箇所に局所塗装する手法である. ジェット射出時, 塗料は射出方向に伸長するため, 射出体積制御には伸長挙動の調査が必要である. しかし, 塗料は多数の成分を含む複雑流体である. そのため伸長挙動の予測・評価が難しく, 射出体積制御の障害となる. 一方でせん断粘度測定装置は広く普及している. 塗料のせん断粘度から伸長挙動を推定できれば，ジェットの伸長レオロジーの議論が容易になる. しかし, 塗料のせん断粘度と伸長挙動の関係は物理的根拠によって示されていない. そのため, 塗料のせん断粘度と伸長挙動を測定し, それらの関係を調査する必要がある.

　本研究は, 車体塗料の液糸ネック半径の時間推移 (伸長挙動)，伸長粘度の伸長速度変化, せん断粘度のせん断速度変化を測定し、それらの関係を解明することを目的とする.

2.　実験方法

　本実験では, 製造後3ヶ月以内の車体塗料 (normal) および使用期限超過の車体塗料を使用した. 使用期限超過の塗料は劣化して二層に分離しており, 低粘度の上澄 (top) と高粘度の沈殿 (bottom) の測定を行なった.

　CaBER-DoS⁽²⁾の実験装置図を図1に示す. ノズルから押し出された液体がガラス板に付着すると, 液体はガラス板上で濡れ広がり, 液糸を形成する. 表面張力γの作用で液糸は徐々に細くなり, 千切れる. この液糸の様子を高速度カメラ (FASTCAM SA-X, Photron, 空間解像度3.5 μm/pix) で撮影した (図2). せん断粘度測定には, せん断レオメータ (AR-G2, TA Instruments) を使用した.

3.　実験結果および考察

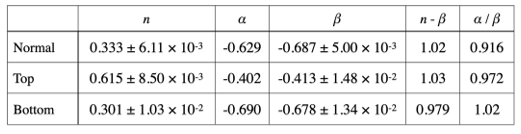
　液糸ネック半径Rの時間推移, 液体の表面張力を測定することで, 伸長速度と伸長粘度が算出可能である⁽²⁾. 車体塗料の液糸ネック半径Rの時間推移 (図3(a))，伸長粘度の伸長速度変化 (図3(b)) を測定・算出した結果, べき乗で記述できることが明らかとなった. せん断粘度のせん断速度変化を測定した結果 (図3(b)) もべき乗で記述できることから, 塗料はshear-thinning性であることがわかった. それぞれのべき乗指数は塗料の状態によって変化した. 液糸ネック半径Rの時間推移に関する指数をn, 伸長粘度の伸長速度変化に関する指数をα,せん断粘度のせん断速度変化に関する指数をβとする(表1). 本実験から, n – β ~ 1, α ~ β, n – α ~ 1が成り立つことが確認できた. n – β = 1 , α = βは, 理論式から導出可能である^{(3) (4)}. この2式からせん断粘度と伸長挙動に関する指数の関係がわかり, n – α = 1である. つまり, 塗料の伸長挙動は, せん断粘度から推定可能であることが実験的, 理論的に明らかとなった.

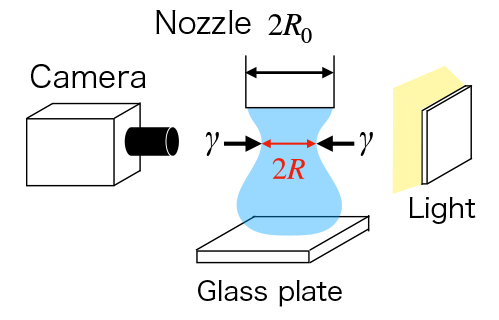
Figure 1  Experimental setup for the measurement of extensional rheology.

Figure 2  Image sequences which show a filament of coating

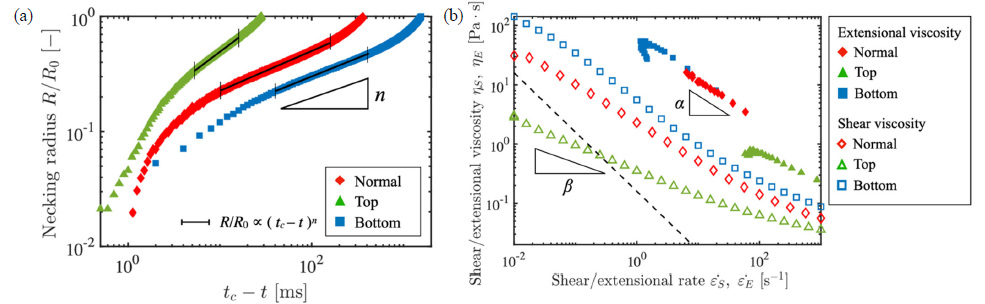
Figure 3  (a) Neck radius evolution R/R₀ versus time t_c-t, (b) Extensional viscosity η_E versus extensional rate  and shear viscosity η_S versus shear rate \(\dot{ε}\)_s.

Table 1  Values of the exponents.

4.　結　　　言

　本研究は, 産業用塗料のせん断レオロジーと伸長レオロジーの関係を特徴づける因子を明らかにすることを目的とした. 塗料はshear-thinning性を有する. 液糸ネック半径Rの時間推移から得られる指数n , せん断レオロジー測定から得られる指数α, 伸長レオロジー測定から得られる指数βには, n – β = 1, α = βの関係があることを実験的, 理論的に確認できた. つまり, 車体塗装の実用化の面で重要となるn – α = 1 の関係が得られた.

謝　　　辞

　末筆になりますが，本発表に際してご聴講くださった皆様，貴重なご意見を頂いた先生方に心から感謝申し上げます. 重ねて, 優秀講演表彰を授賞してくださった選考委員の先生方，今回のニュースレターの執筆機会をくださった日本機械学会流体工学部門関係者の皆様に心より御礼申し上げます．

文　　　献

(1)	Onuki H. and Tagawa Y., “Microjet generator for highly viscous fluids”, Physical Review Applied, Vol. 9 (2018), 014035.
(2)	Dinic J., Jimenez L. N. and Sharma V., “Pinch-off dynamics and dripping-onto-substrate (DoS) rheometry of complex fluids”, Lab on a Chip, Vol. 17 (2017), pp. 460-473.
(3)	Clasen C., Phillips P. M., Palangetic L. and Vermant A. J., “Dispensing of Rheologically Complex Fluids: The Map of Misery”, AIChE Journal, Vol. 58, No. 10 (2012), pp. 3242-3255.
(4)	Coussot P. and Gaulard F., “Gravity flow instability of viscoplastic materials: The ketchup drip”, Physical Review E, Vol. 72, No. 3 (2005), 031409.