流れ　2022年3月号　目次

―　特集テーマ： 流体工学部門講演会　3月号　― 巻頭言 （橋本，松田，朴） 印象派物理学への誘い：流体・界面などの研究から 奥村 剛（お茶の水女子大学） 遠心羽根車の回転円板と静止円板間の隙間流れと摩擦トルクの関係 阪井 健人，稲葉 夢乃，宮川 和芳（早稲田大学），佐野 岳志，前田 聡（三菱重工業株式会社） べき乗則流体の伸長レオロジーとせん断レオロジーの関係 松本 祐月（東京農工大学），田川 義之（東京農工大学） 火炎旋風の魅力 田中　実（明星大学） 　｜　リンク一覧にもどる　｜

 

遠心羽根車の回転円板と静止円板間の隙間流れと摩擦トルクの関係

阪井 健人， 稲葉 夢乃， 宮川 和芳 （早稲田大学）， 佐野 岳志， 前田 聡 （三菱重工業株式会社）

1.　はじめに

　令和3年11月に開催された日本機械学会第99期流体工学部門講演会において，光栄にも若手優秀講演フェロー賞を頂いた．この場をお借りして，選考委員会の皆様および日本機械学会流体工学部門の皆様に御礼を申し上げるとともに，講演発表内容を以下に紹介する．

2.　緒　　　言

　小型・高揚程の単段遠心ポンプの設計では，低比速度化により増加する円板摩擦損失の低減が高効率化に向けた課題であり⁽¹⁾，回転円板と静止壁面の隙間流れに関する理論的研究は従来から行われている⁽²⁾．また著者らのグループは回転円板の表面形状が与える流れ場への影響を調査し，抵抗損失の低減手法を提案している⁽³⁾⁽⁴⁾．しかし産業界での応用は少なく，損失低減手法の構築にあたっては円板間の狭い隙間における流れ場の把握が重要である．本研究では遠心羽根車背面とケーシングとの間の流れを模擬した回転円板試験装置を用いて，異なる回転数・流量における円板間の隙間流れの圧力分布と摩擦トルクを計測した．またCFD解析結果との比較を通じ，内部流れと摩擦損失の関係について考察した．

3.　概　　　要

3・1　試験装置および試験手法
　図1 に示す試験装置を用いた．試験装置は供試部・耐圧タンク・昇圧ポンプを閉ループで接続しており，供試部である回転円板（直径D=380[mm]）と静止壁との隙間領域は内向き及び外向きの流れとすることが可能である．供試部は遠心ポンプの羽根車背面とケーシングとの間の漏れ流路を模擬し製作し，隙間幅と円板直径の比 S/Dは1%とした．また本試験装置では，回転円板に加わる摩擦トルクおよび隙間領域の半径方向圧力分布を計測可能である．本試験では作動流体は水とし，隙間内流れ方向・円板回転数・流量を変化させた．円板の最大回転数は2000[rpm]，最大流量は外向き流れで4.0[L/s]，内向き流れで1.0[L/s]である．試験中は回転数の変化とともに回流する水の温度に変化が認められたため，試験装置に熱電対センサを接続し水温も併せて測定した．

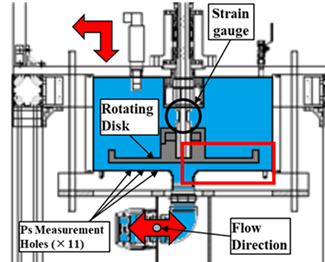
Figure 1　Experimental Equipment

3・2　CFD解析手法
　解析のモデルを図2に示す．解析領域は軸方向隙間内，回転軸付近の配管，円板と水槽側面の間の3箇所とし，回転軸周方向は軸対称とし角度9度を切り出している．要素数約960万の解析領域に対して入口境界に質量流量一定の条件，出口境界に静圧一定の条件を与え，試験における運転条件を模擬する．一部の運転条件で水温の変化の影響を考察する為，異なる水温の物性値を与え複数ケースの解析を行った．乱流モデルにRANS SST k-ωモデル，解析コードにはANSYS CFX 19.2を用いた．

　加えて軸方向隙間比s/Dの影響を調査する為，追加の解析を実施した．計算負荷の観点より解析領域は軸方向隙間内のみとし，s/Dを0.5%～3.0%までに変化させた解析を行った．解析条件については上述と同様である．

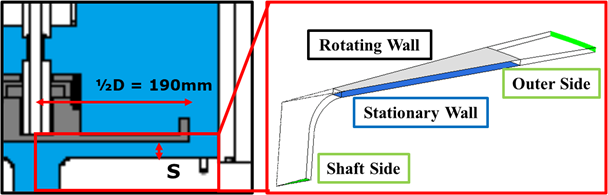
Figure 2　Analysis Domain

3・3　解析結果の妥当性評価
　半径方向の静圧係数分布について流量別に比較したものを図3に示す．運転条件は円板回転数1000[rpm]，隙間比はS/D = 1.0%であり，左から順に外向き，内向き流れと並べた．実験と解析にて静圧係数は定量的に一致し，CFD解析が試験装置での円板間の隙間流れを十分模擬できていることを確認した．

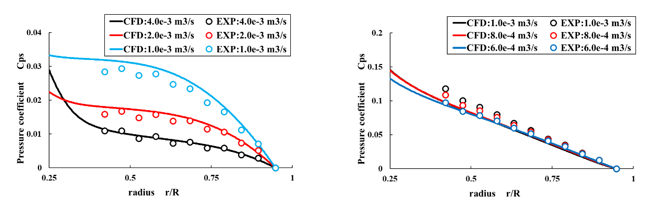
Figure 3　Pressure coefficient distribution in the radial direction (Left: Outflow, Right: Inflow)

4.　摩擦トルクと内部流れの関係

　実験および解析で取得した摩擦トルクは円板摩擦係数として無次元化し評価を行う．円板回転数と円板摩擦係数との関係ではバラつきがみられたため，水温の影響を加味したRe数で再整理を実施した．外向き流れにおける結果を図4に示す．実験と解析で定性的に一致したことから，円板摩擦係数への影響評価には円板の回転数ではなく水温も考慮したRe数での整理が適することが分かった．実験と解析が定量的に一致しなかったのは，実験結果は回転円板上面・側面等に発生するトルクも含むのに対し，解析結果は回転円板底面で発生するトルクのみを表すためである．先行研究での理論解析および実験的研究⁽²⁾⁽⁵⁾では，乱流境界層が十分発達したRe数においては、円板摩擦係数がRe数の-1/5乗に比例することが知られているが，本研究で得られた実験・解析結果でも同様の傾向を示していることを確認した．また大流量側の方が円板摩擦係数は大きくなる傾向も実験結果より明らかになった．

　図5はCFD解析結果における円板間隙間流れの流線および全圧係数のコンター図を各解析条件で比較したものである．具体的には(a)と(b)では水温が異なるが回転数が同一の場合，(b)と(c)では回転数と水温がそれぞれ異なるが概ねRe数が同一の場合を比較している．はじめに(a)と(b)を比較すると，水温の高い(a)の方が僅かに内径側から渦が形成され，最外径に存在する中心渦も大きい傾向が確認できる．隙間内の渦の存在は隙間内の速度勾配を小さくするため⁽⁴⁾，発生渦がより大きい(a)の方が円板摩擦係数は小さくなったものと考えられる．次に(b)と(c)を比較すると，回転数の小さい(c)は最外径に小さい渦がみられる程度で，(b)の渦と比較しても大きさ・発生領域が異なっている．渦の大きさが異なり隙間内の速度勾配に差がありながら，(b)と(c)が同程度のRe数，つまり同程度の円板摩擦係数である理由は，(c)は流体の粘性が低く渦の発生領域以外での流体摩擦量が影響するためである．

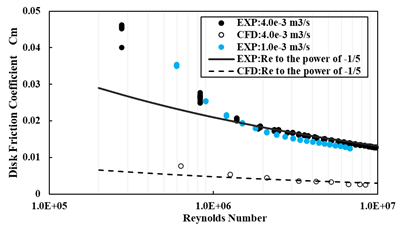
Figure 4　Pressure coefficient distribution in the radial direction (Outflow)

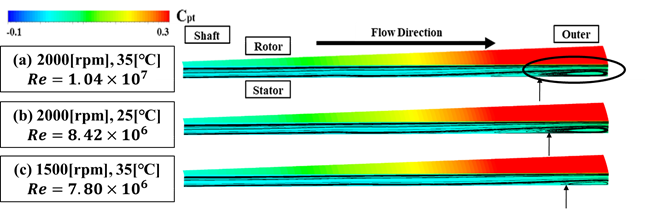
Figure 5　Total Pressure coefficient distribution and streamline (Outflow,Q = 4.00×10^-3[m³/s] )

5.　軸方向隙間比が与える摩擦トルクへの影響

　図6に軸方向隙間比と円板摩擦係数の関係を示す．外向き流れではS/D = 0.4％程度で円板摩擦係数は極小値をとる．一方で内向き流れでは隙間幅が大きくなれば円板摩擦係数は小さくなり，S/D = 1％程度を境に一定値に漸近する．隙間幅が小さいと流れ方向によらず円板摩擦係数が急増し，回転数による違いはみられない．

　図7は隙間内半径方向速度の分布を3種類のS/Dで比較したものである．横軸は静止壁からの隙間方向の無次元距離を示し，縦軸で示す半径方向速度は子午面速度で無次元化されている．まずS/D=0.1%では，隙間内の半径方向速度分布に大きな違いがみられない．次にS/D＝0.4%では，内向き流れは静止壁側の流速が増加するのに対し，外向き流れでは回転壁側の流速が増加する．最後にS/D＝2.0%では，円板外周側の静止領域において逆流が発生している．この逆流により主流流速が増大し円板摩擦損失の増加に繋がったと考えられる．また図8に隙間内の接線方向速度の分布を示す．ここで縦軸の接線方向速度は回転円板の周速度で無次元化されている．軸方向隙間比が大きいS/D＝2.0%の場合，回転円板と静止円板にて発生する境界層の間に周方向速度が一定のポテンシャルコアの生成が確認でき，外向き流れにおける円板摩擦係数の増加の一因となっている．一方軸方向隙間比が小さいS/D＝0.1%の場合，両壁面の境界層が干渉し円板摩擦係数は増加する．S/D＝0.4%ではポテンシャルコアが消滅し境界層干渉も発生しないため，外向き流れでは円板摩擦係数が最小となったと考えられる．

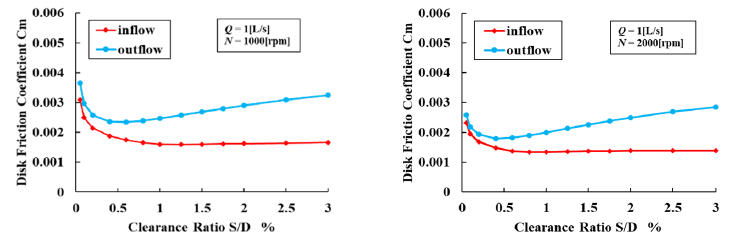
Figure 6　The influence of clearance ratio S/D on disk friction coefficient

Figure 7　Radial velocity distribution

Figure 8　Tangential velocity distribution

6.　結　　　語

　回転円板試験装置を用いた試験と数値解析を実施し，主に回転レイノルズ数・軸方向隙間比が及ぼす円板摩擦係数への影響について考察した．円板の回転数は隙間内の渦形成に伴う速度勾配の変化，水温は動粘性係数の変化という点で円板表面に働く摩擦抵抗に加えて渦サイズにも影響を与え，結果的に円板摩擦係数が変化する一因となることを示した．また軸方向隙間幅が小さければ両壁面の境界層の干渉が，大きければ外向き流れの場合は隙間内の静止壁側での逆流の発生が，それぞれ円板摩擦損失の増加に繋がることを示した．

謝　　　辞

　本研究(の一部)はWISE(早稲田理工学術院総合研究所)のプロジェクト研究「水力ターボ機械システムの高性能化、高信頼性化研究」の一環として実施した．

文　　　献

(1)	Stepanoff, A. J., “Specific Speed and Design Constants,” Centrifugal and Axial Flow Pumps, pp. 68-89, (1957).
(2)	黒川，豊倉，“遠心型ターボ機械の漏れ損失および円板摩擦損失について”，ターボ機械4巻5号，pp.302-310, (1976).
(3)	R, Ujiie et al. “Influence of clearance flow on disk friction loss in low specific speed hydraulic machines”, IOP Conference Series: Earth and Environmental Science, Volume 240, Issue 3 (2019)
(4)	Y, Inaba et al. “Investigation of Flow Structure in a Narrow Clearance of a Low Specific Speed Centrifugal Impeller”, Journal of Fluids Engineering, FE-21-1166, (2021)
(5)	Daily, J.W. et al “Chamber Dimension Effects on Induced Flow and Frictional Resistance Enclosed Rotating Disks”, Trans.ASME, 82-1, 217, (1960)