流れ 2023年2月号 目次
― 特集テーマ：流体工学部門講演会 2月号 ―
｜ リンク一覧にもどる ｜ |
多相系の乱流の数値シミュレーション（統一体積平均方程式に基づくモデリングの試み）
|
１．まえがき
流れの数値シミュレーションでは，直接計算されない現象の効果を表す物理モデルの構築に多大の努力が積み重ねられてきました（ここでは，離散化してプログラミングするために構成された支配方程式群を計算モデル，その中で用いられる，直接計算されない現象を近似する数式群を物理モデルと称することにします）．しかし周知のとおり，乱流に対しても，多相流に対しても，広範囲の条件に適用できる普遍的な物理モデルは完成していません．これに対して，計測との連携や機械学習の導入などにより，計算の解像度やモデルの不備の問題を補完した高度な予測手法の研究が最近では盛んに行われています．
現在の最先端の大規模計算機でも，工業装置や自然界の流れの現象をフルスケールで扱うには容量が全く足りません．そのため，粗視化された基礎方程式に基づき，直接計算できない小スケールの現象の効果を表す項に物理モデルを与える必要があります．加えて，計算領域より大きなスケールに対して，境界条件としてモデルを与える場合もあります．物理モデルの高度化も，データサイエンスとの融合も，適切に粗視化された支配方程式に基づいて検討されなければなりません．
２．粗視化の統一に向けて
乱流の非定常計算法として標準的になりつつあるLarge-Eddy Simulation（LES）は，明確に定義された空間フィルターによって粗視化された変数の微分方程式を扱います．しかし，格子幅に関連づけられるフィルター幅は空間的に変化するため，微分操作とフィルター操作の順序は互換的ではありません．現状のLESで用いられる計算モデルは一般に，その差から生じるcommutation errorを含んでいます．これに対して，容易にプログラミングできる解決法はなく，難しいことは重要ではないとして無視しているのが実態です．実際，空間的に一様な方向にあえて非一様な格子で計算してみると，その影響は軽視できないことがわかります．
多相流においても，各相の体積率などの平均量が用いられることがあります．例えば計算格子を検査体積と定義すれば平均量は数学的には明確ですが，そこに使われる物理モデルはそのように粗視化された量で成り立っているわけではありません．あるいは，気泡や粒子を質点で近似することもありますが，計算格子で求める流れ場との相互作用の際にスケールのずれが生じます．多相系の乱流に関しては，それぞれの分野で都合の良い平均化，それぞれの分野に存在する物理モデルを掻き集めて計算モデルを作っているのが現状と言えます．これでは広範な条件に適用できる予測手法としても，現象の解明ための解析手法としても不十分です．
本稿では固体粒子群を含む乱流の数値シミュレーションに焦点を当てます．粒子の混入による乱流の変化（乱流変調）は古くから研究されていますが(1)(2)，支配因子は整理されておらず，乱流変調を表すモデルは確立されていません．したがって，当面の課題は乱流変調の再現と解明ですが，われわれは物理モデルを用いた予測と制御まで視野に入れ，一貫性のある計算方法の構築を意図しています．一般には，固体粒子の形状やサイズも，乱流計算のための格子も一様ではありません．乱流の直接数値シミュレーション（DNS）を想定しても，粒子の周りの流れを格子である程度とらえられる場合（図1左）もあれば，質点モデルを使わざるを得ない（むしろ適している）場合（図1右）もあります．図2に示す固液二相自然対流(3)(4)は講演で紹介した前者の計算例です．
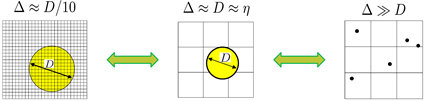
Fig.1 Various relationships among partile diameter 
, Kolmogorov scale 
of background turbulence and grid width 
for computation of fluid low
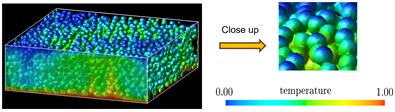
Fig.2 A snapshot of natural convection at Rayleigh number 
of solid-liquid two-phase media including 3087 spherical particles (volume ratio 30.8%)(3)
乱流変調の研究の大きなテーマとして，コルモゴロフスケールに近い径の粒子群の影響があります．この場合，単相乱流のDNSのための格子幅と粒子径は同程度（図1中）となります．乱流変調の系統的な研究のためには，この状況を含み，図1の幅広いスケール関係を一貫して統一的に扱う数値解析法が必要です．また，現象解明の計算と工学的実用の計算では，直接計算するスケールと物理モデルを使うスケールが変わるだけで，計算法に求められる事柄は共通です．したがって，前段で長々と述べたように，乱流と多相の双方に対して明確かつ統一的な粗視化が不可欠となるわけです．
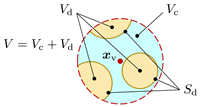
Fig. 3 Control volume for the construction of unified averaging for multiphase flows
図3のように代表点
を囲む検査体積
を定め，そのうち流体（連続相，添え字
）と固体粒子（分散相，添え字
）が占める領域をそれぞれ
と
で表します．各相の体積率を
（
, ただし
），検査体積内にある分散相の表面を
とします．ここでは両相とも非圧縮であるとします．単位体積あたりの物理量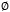
に対して，点
において相ごとの平均値
を定めます．平均操作と微分操作の関係(5)に注意すると，連続相の質量保存式と運動方程式は次のように表されます．
詳細は後掲の文献(6)~(10)に譲るとして，モデル化が必要となる主要な項は，連続相の速度変動に起因する残余応力
（ただし
）と粒子との相互作用力
です．前者は乱流のレイノルズ応力に似た形です．後者は検査体積内にある粒子表面の応力に起因します．そこで手始めに，
には従来の渦粘性モデル，
における表面積分にはStokes流れなどの解析解から拡張したモデルを適用してみたところ，粗視化された流れ場や粒子の軌跡の再現性において希望の持てる結果となりました．具体的には，図1中のように格子幅と同程度の粒子径を扱っても，渦の中の粒子の軌跡が高解像度のDNSの結果と，粒子懸濁液における剪断応力の増加が理論値と，それぞれ良好に一致しました．その理由は，図3から推察できるように，検査体積に含まれる粒子表面
の応力だけが代表点
での流体の体積平均速度に作用する形になっているからであり，粒子表面の応力分布が適切に流体に反映されたものと考えています．このように，粒子と流体に対して整合性のある平均化と微分操作に基づいた計算法を使えば，粒子径と格子幅の比に対してかなり広範に，多相系の乱流に対して効率的な計算ができる見通しが得られました．
３．これまでの進展と展望
時空間的に様々な粗視化の考え方がありますが，ここでは将来的に多相乱流のLES手法にまとめることを意識して局所体積平均を採用しました．式の導出や各項のモデリングおよび数値計算法については公表済みの論文を紹介するにとどめます： 格子幅と同程度の径の固体粒子を含む流れを解析できる体積平均方程式と相互作用項の導出(6)； 体積平均方程式を用いて粒子と渦の相互作用を数値解析する方法の提案(7)； 体積平均方程式により流体・粒子のtwo-way解析するための流体力の評価(8)； 格子幅より小さい粒子にはたらく流体力の非等方性の体積平均方程式への反映(9)； 固体粒子を含む乱流におけるサブグリッドスケールモデルの検討(10)．以上より，既存のモデルを使える範囲内では，基本的な考え方の妥当性は実証されたと思います．今後，粒子と流体の相対速度に基づくレイノルズ数が高い場合の相互作用モデル，流体を介した粒子間の相互作用モデル（潤滑の問題）については，かなり根気を要する研究になりそうです．ただし，将来的に想定される機械学習などの援用に際しても，明確な平均操作に基づく粗視化方程式の重要性を示すことができたのではないかと考えています．
謝辞
新型コロナウィルスの感染状況が小康状態ではあったものの，困難な状況下で記念すべき第100期流体工学部門講演会の対面形式での実現に尽力されました川原顕磨呂先生，宗像瑞恵先生をはじめとする実行委員会の各位に敬意を表すとともに，筆者に基調講演の機会をいただきましたことに感謝申し上げます．また，本稿で紹介した成果は，大阪大学工学研究科の竹内伸太郎准教授および電力中央研究所の深田利昭博士との共同研究によるものであることを書き添えます．