流れ 2023年2月号 目次
― 特集テーマ：流体工学部門講演会 2月号 ―
｜ リンク一覧にもどる ｜ |
遷音速軸流圧縮機における動静翼列干渉の大規模DES解析
|
0. はじめに
日本機械学会 第100期 流体工学部門講演会において，光栄にも若手優秀講演フェロー賞を頂いた．この場を借りて，日本機械学会の皆様ならびに選考委員会の皆様に深く御礼申し上げる．本ニュースレターでは，講演発表内容を以下に紹介する．
1. 緒言
多段軸流圧縮機は産業用および航空用ガスタービンにおける主要構成要素の一つであり，昨今ガスタービンの熱効率向上を目指して圧縮機の高負荷および高圧力比化が求められている．それに伴い，圧縮機内部では遷音速流れ場が形成され，衝撃波によって速度，圧力，密度などのすべての物理量が急変化する．さらに，衝撃波と翼端漏れ渦や翼面境界層との干渉により，内部流れ場は極めて複雑な様相を呈する．特に圧縮機上流動翼の翼端付近では強い衝撃波が発生するため，設計段階において衝撃波の発生位置だけでなく衝撃波と翼端漏れ渦および翼面境界層との干渉も予測することが求められる．しかしながら，このような遷音速軸流圧縮機内の流れ場を試作実験のみで詳細に解明するのは困難であるため，近年ではコンピュータによる数値計算を用いて内部の流れ場を解析する数値流体解析（CFD）が盛んに行われている．
また，多段遷音速軸流圧縮機では，上流・下流翼列の時々刻々と変化する位相関係に伴って，後流干渉やポテンシャル干渉，衝撃波干渉などの動静翼列干渉が発生する．近年では，軽量化・小型化と高負荷・高圧力比化の両立を目指した薄翼の採用や短軸長設計が散見され，動静翼列干渉に起因する高サイクル疲労による翼損傷トラブルが増加している．その対策として設計段階で動静翼共振の振動を高精度に予測することが必要不可欠であり，圧縮機の全周・全段を対象とした大規模な三次元CFDを用いた詳細な解析が必要となる．
そこで，本研究では，産業用ガスタービンに用いられる多段遷音速軸流圧縮機の全周・全段を対象に大規模DES（Detached Eddy Simulation）解析を実施した．また，得られた解析結果に対して，知的可視手法を用いた三次元渦流れ構造の分析および位相固定平均化手法を用いた動静翼列干渉効果の抽出を行った．
2. 計算格子
本研究における解析対象は，入口案内羽（Inlet Guide Vane，以下IGV），初段動翼，初段静翼から構成される遷音速軸流圧縮機である．計算格子は，クリアランスを含め全てH-O型を組み合わせた格子トポロジーによるマルチブロック構造格子で作成した．本解析において，フィレットおよびクリアランスは忠実に再現している．格子生成では，翼周りにO型格子を用いることで翼面付近における格子直交性を高めている．
格子点数は，IGVにおいて上流領域を含め1ピッチあたり約626万点，初段動翼で1ピッチあたり約490万点，初段静翼は下流領域を含め1ピッチあたり約450万点であり，全周で約4.5億点である．なお，計算格子における壁面上の最小格子幅はy+<1を満足するように十分小さい値を設定した．このことは，壁面に隣接する計算セルが粘性底層内に位置していることを示している．
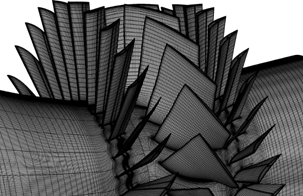
Fig.1 Computational grid (every three line)
3. 計算スキーム
本研究では，k-
二方程式モデルベースのDES(1)による非定常計算を実施した．非定常三次元圧縮性Navier-Stokes方程式を支配方程式とし，セル中心型の有限体積法に基づいて離散化した．非粘性流速の評価には，SHUS（Simple High-resolution Upwind Scheme）(2)を用い，三次精度のMUSCL法（Monotone Upstream-centered Scheme for Conservation Laws）(3)を組み合わせることで空間解像度を高めた．時間方向はEuler陰解法により離散化し，時間積分にはMFGS陰解法（Matrix Free Gauss-Seidel）(4)を用いた．各時間ステップにおいてニュートン反復（5回）を実施し，時間精度を最大二次精度としている．本研究では，遷音速軸流圧縮機における非定常流動現象を適当に捉えるために，非定常解析における時間刻み幅を，平均クーラン数が2.0程度になるような小さな値に設定した．具体的には，動翼1回転当たり90,000時間ステップとした．
4. 数値解析結果
4・1 圧縮機全体の非定常流れ場
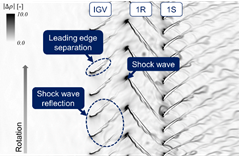
図2にDES解析における瞬時の流れ場から算出した，80%スパン断面における密度勾配分布を示す．図2より初段動翼では隣接翼の離脱衝撃波が負圧面前縁付近で確認された．上流へ伝播した衝撃波はIGVの翼間に流入し，IGVの負圧面上で反射している様子が確認された．また，後流干渉も発生しており，初段動翼の後流が初段静翼に流入することで翼面境界層と干渉している．
|
|
Fig. 2 Density gradient contours at 80% span (left : snapshot, right : animation) |
|
4・2 動静翼列干渉効果
本研究では，遷音速多段軸流圧縮機における翼列間の相対位置関係の変化が流れ場に及ぼす影響について調査するために，位相固定平均化処理を行った．位相固定平均化処理とは，ある翼列間に着目して，非定常解析結果から着目している翼列間の位相関係が同じ瞬間のデータを抽出し，それらをアンサンブル平均化することで，各位相関係に応じた時間平均流れ場を抽出する手法である．本研究では入口案内羽に着目し，非定常DES解析結果に位相固定平均化手法を施すことで，初段動翼の位相変化が入口案内羽に及ぼす影響について調査した．なお，1つのフェーズにおけるアンサンブル数は約200であり，クロッキング角度における
に等間隔に30フェーズ設けてある．
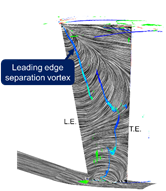
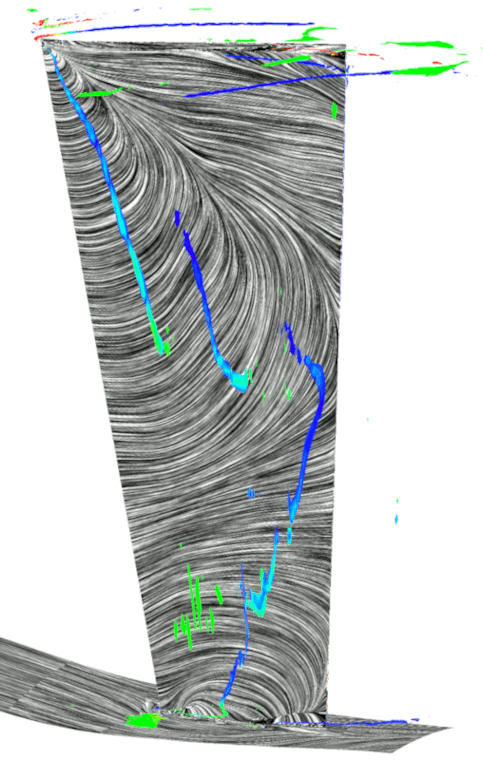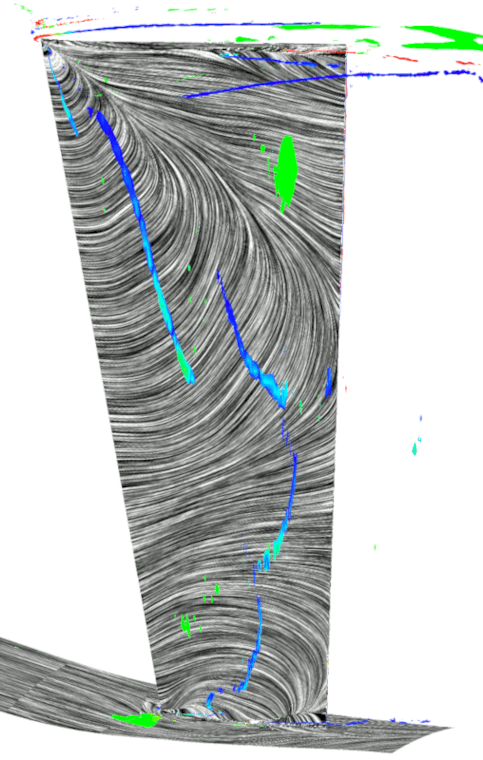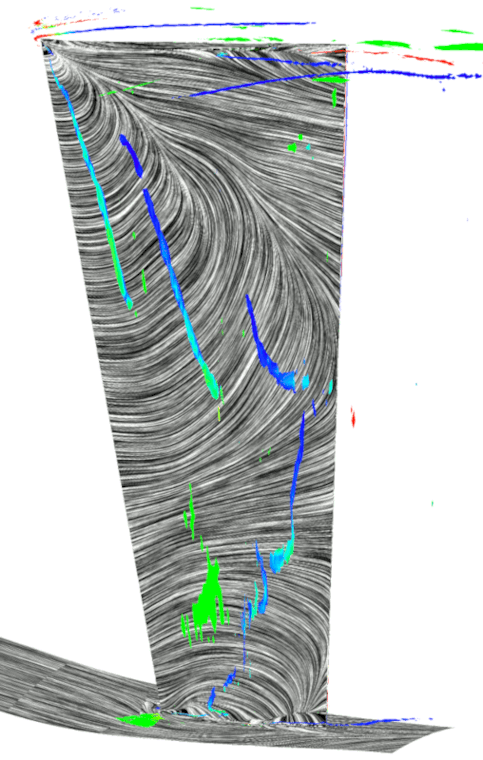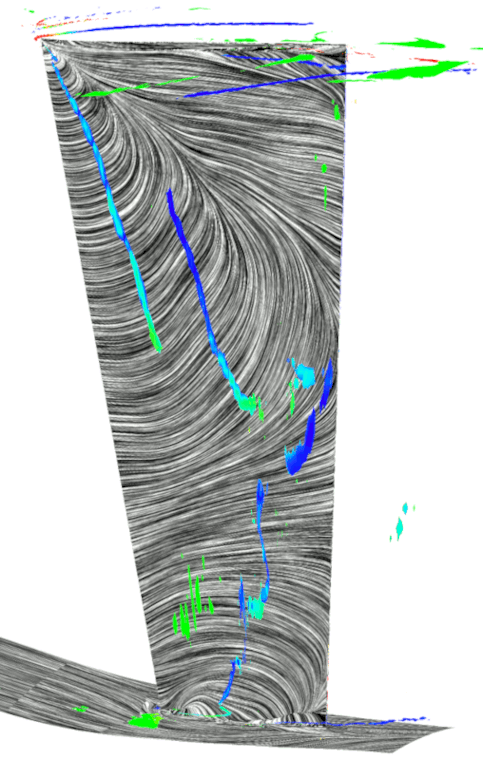
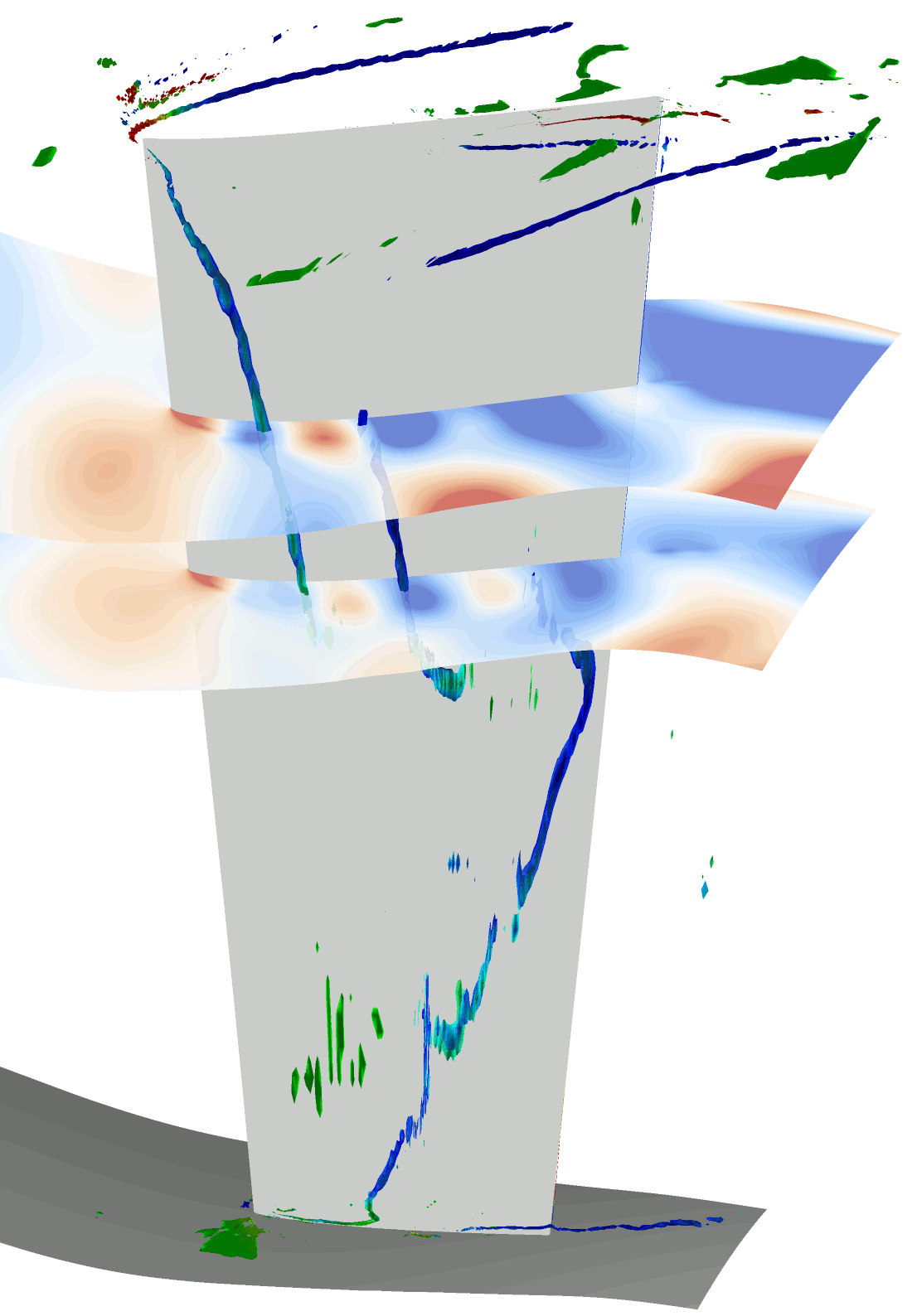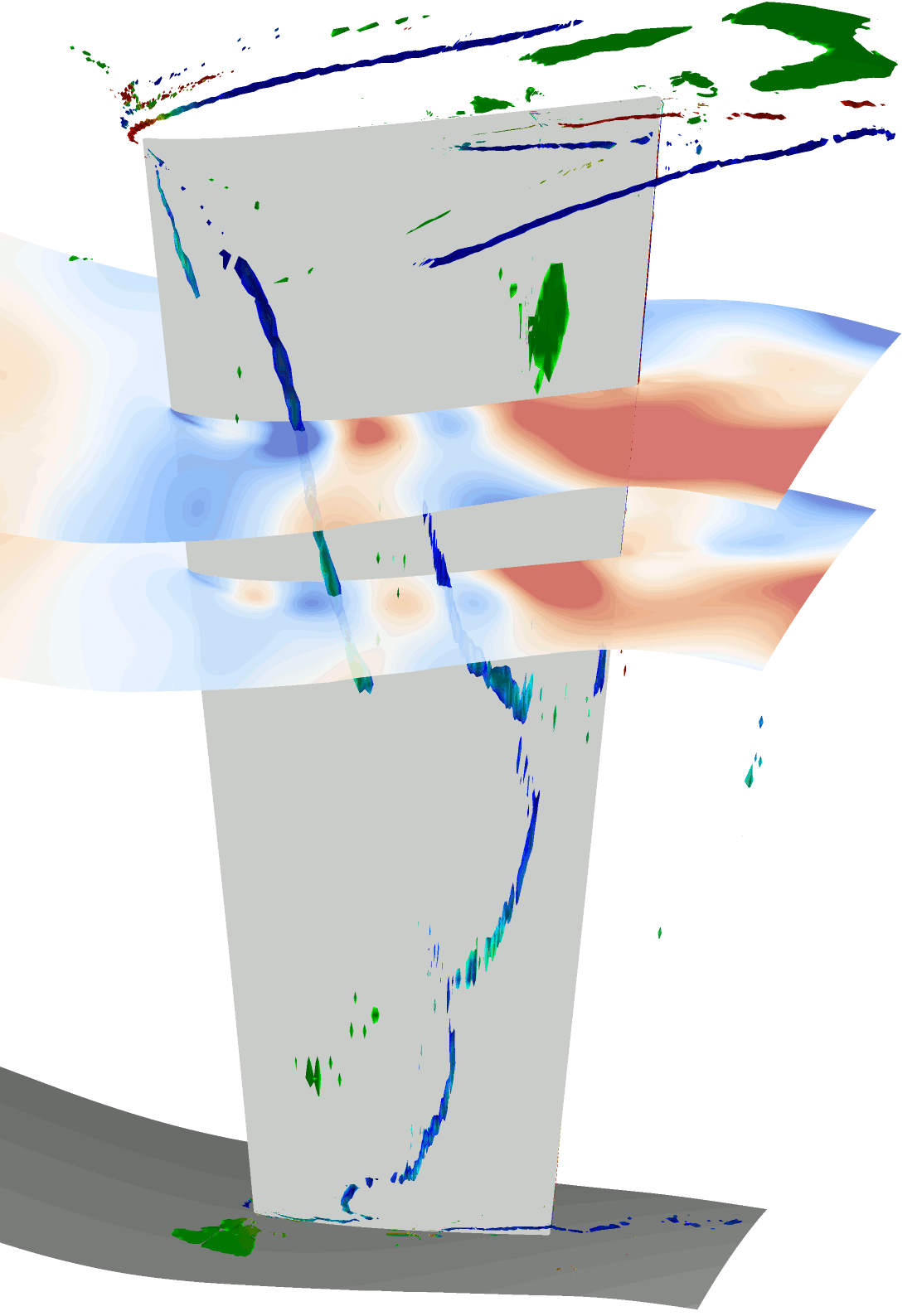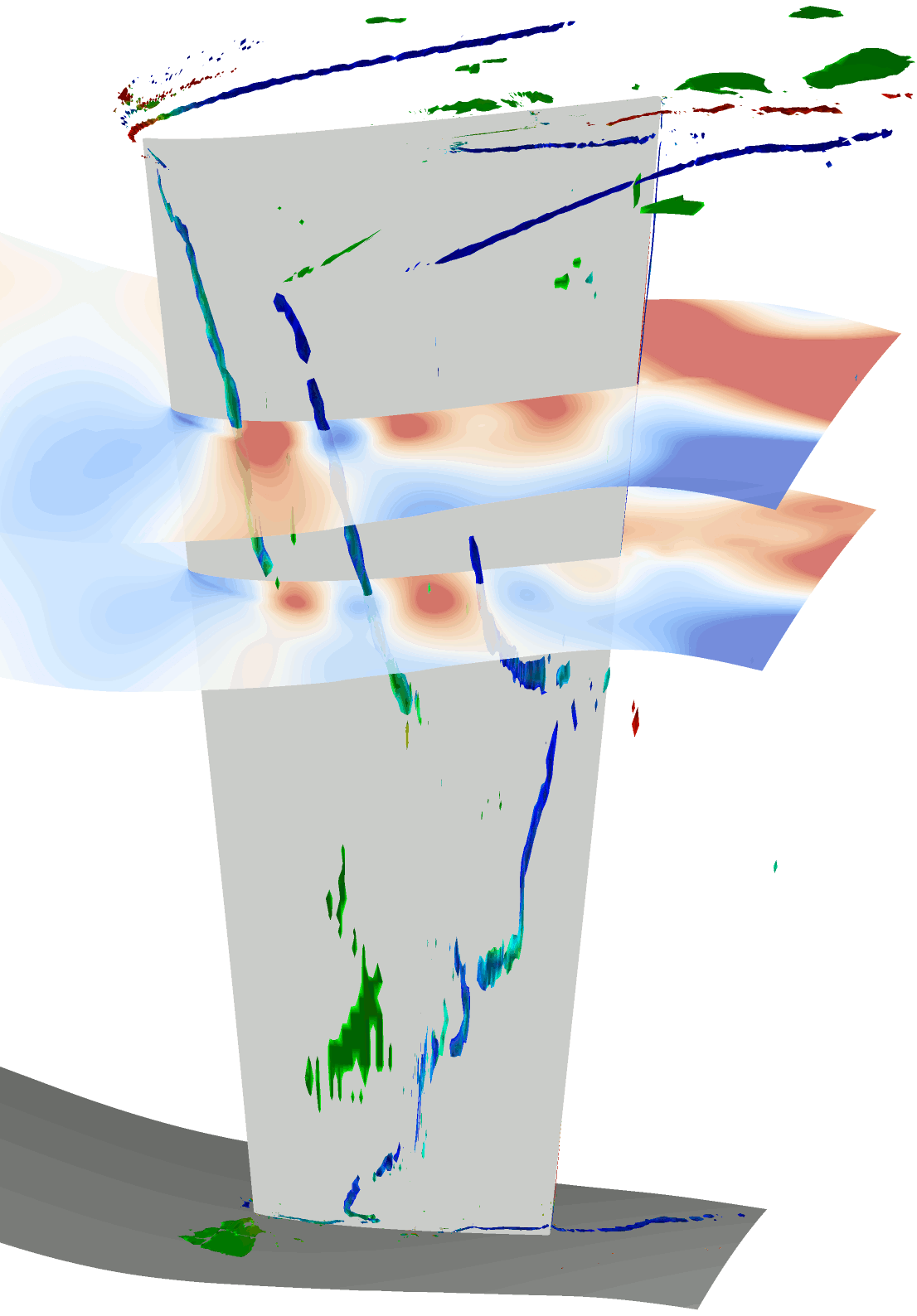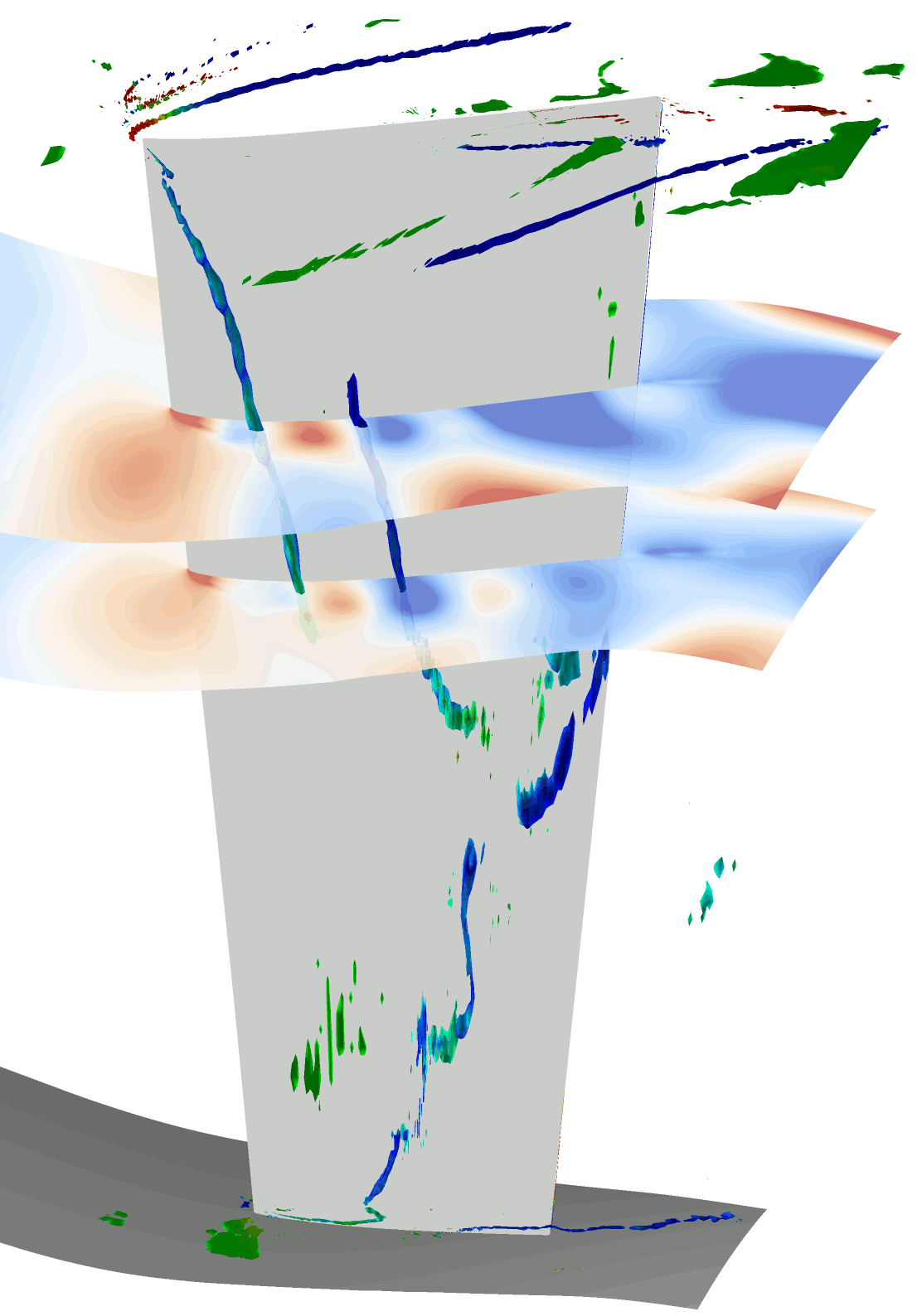
図3に位相固定平均化処理を施した各クロッキング位置におけるIGV負圧面側の時間平均流れ場を示す．同図には，無次元ヘリシティで色付けした渦コア(5)およびLIC法を用いて描画した限界流線を表示している．
|
|
|
|
|
(a) |
(b) |
(c) |
(d) animation |
|
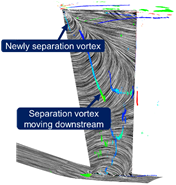
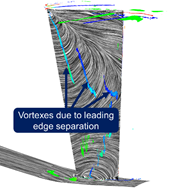
Fig.3 Flow fields at each clocking angle |
||||
図3から，位相固定平均処理を施し各位相関係における流れ場を可視化することで，初段動翼の翼通過に伴って流れ場が変化していることが確認された．IGVの負圧面で発生している前縁はく離渦は，初段動翼の位相変化に伴って分裂・移流を繰り返しており，シュラウド側の翼端漏れ渦は発生と消滅を繰り返していることが確認された．以下に前縁はく離渦の挙動に関して詳細を述べる．
図3より，
において負圧面の50%スパンからシュラウド側にかけて前縁はく離渦が発生していることが確認される．時間が経過して
になると，前縁はく離渦はシュラウド側で二つに分裂する．これは，50%スパン付近のはく離渦は下流に移流しているのに対して，シュラウド側のはく離渦は前縁近傍に定在しているためであると考えられる．
においては，新たに発生したシュラウド側の前縁はく離渦が成長しハブ側へと延長され，前縁はく離渦に由来するはく離渦が3つ確認される．これらの前縁はく離渦が分裂し移流する現象は初段動翼の翼通過と同じ周期で発生しているため，初段動翼との動静翼列干渉による影響であると考えられる．
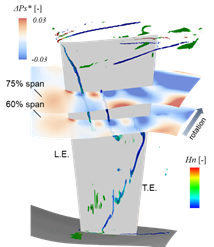
図4に位相固定平均結果より算出した無次元ヘリシティで色付けした渦コア(5)と，60%,75%スパン断面における圧力変動分布を表示している．また，圧力変動値
が0.03を示すとき，時間平均値より3%圧力が高いことを示す．この図より，前縁はく離渦に起因する低圧領域が上流から移流していることが分かる．一方，初段動翼とのポテンシャル干渉に起因する高圧領域が下流側から上流側に伝播し，それらが相殺し合うことで，負圧面上に圧力変動の小さい領域が存在している．これより，初段動翼のポテンシャル干渉がIGVの流れ場に強く影響を与えていることが確認された．
 |
|
Fig. 4 Pressure variation contours and flow fields (left : snapshot, right : animation) |
|
5. 結言
本研究では，産業用ガスタービンに用いられる多段遷音速軸流圧縮機の動静翼列干渉について調査するために，全周・全段を対象としたDES解析を実施し，共振点における流れ場を解析した．また，得られた解析結果からIGVと初段動翼の動静翼列干渉について調査した．得られた知見は以下の通りである．
- 瞬時の流れ場を可視化することで，非定常流れ場を調査した．後流干渉が確認され，IGVおよび初段動翼の後流が下流翼列に流入し，翼間の流れ場に影響を及ぼしている．また，初段動翼で発生した膨張波および衝撃波は上流のIGVへ入射し，翼面で反射している．初段静翼の負圧面側では大規模なハブ・コーナーはく離が発生し，時間的に大きく変化している．
- 得られたDES解析結果に対し，位相固定平均化処理を施し初段動翼の位相変化がIGVに及ぼす影響を調査した．初段動翼の位相変化に伴ってIGVの翼間を高圧領域と低圧領域が交互に伝播しており，前縁付近の速度場が変動することで前縁はく離渦は分裂・移流を繰り返す周期的な挙動を示す．これらの周期的な流れ場の変動は初段動翼の翼通過と同じ周期で発生しており，初段動翼とのポテンシャル干渉によりIGV周りの流れ場が周期的に変動していることが分かった．
謝辞
本研究における数値計算は，九州大学情報基盤研究センターのスーパーコンピュータシステムITOを利用して実施した．ここに記して謝意を表する．