流れ 2023年2月号 目次
― 特集テーマ：流体工学部門講演会 2月号 ―
｜ リンク一覧にもどる ｜ |
固体粒子の添加による壁乱流の変調現象
|
1. 緒言
この度は，日本機械学会第100期流体工学部門講演会にて優秀講演表彰をいただきました．この場を借りて，選考委員会および日本機械学会の皆様に感謝申し上げます．このニューズレターでは，本講演会で発表しました研究内容について紹介いたします．
本研究では，有限の大きさをもつ固体粒子を添加することによる壁乱流の変調現象を調べます．粒子を乱流に添加すると，乱流がおとなしくなったり，余計に乱れたりすることはよく知られています(1)．しかし，乱流と粒子の相互作用を特徴づけるパラメータが多く，それらを系統的に変えた結果が少ないため，どのような種類の粒子をどのくらい入れると，乱流のエネルギーがどの程度増減するのかは，さまざまな提案(2-4)がされているものの完全にはわかっていません．そこで，我々は，数値シミュレーションを駆使し，粒子のパラメータを系統的に変えることで，粒子による乱流の変調現象を紐解きます．
2. 直接数値シミュレーション
系統的な数値解析には，スーパーコンピュータ上で効率よく実行できる数値シミュレーションプログラムの開発が必須です．我々は，2枚の平板状の壁の間に一定の圧力勾配で駆動される流れと，この流体中に分散させた球状の剛体粒子の運動を連成して解く数値シミュレーションプログラムを開発し，大規模な並列計算が可能な富岳や自然科学研究機構のプラズマシミュレータといったスパコン上で実行しました．流体の運動に対しては，ナビエ・ストークス方程式と連続の式を有限差分法を用いて数値的に解き，粒子と流体の相互作用は埋め込み境界法(5) という粒子の周りの流れを解像する手法を用いて評価しました．
まず，粒子を添加せずに，（摩擦速度
と平板間距離の半幅
，動粘性係数
で定義される）摩擦レイノルズ数
が
，
，
の乱流をシミュレートします．これらの発達した乱流場に，ある大きさと質量密度をもつ粒子を添加し，各粒子によって乱流がどの程度変調するのかを調べます．具体的には，（壁摩擦長で規格化した）粒子の直径
を，乱流中の最も小さな渦の直径程度（
）から，平板間の距離程度の大きさ（
）までの範囲で変え，さらに，流体に対する粒子の質量密度比（
－
）も変えて，合計
種類の粒子の数値シミュレーションを実施します．ただし，十分に希薄な場合を考え，粒子が流体中に占める体積割合
はそれぞれのレイノルズ数（
%－
%）で固定し，また，重力の影響も無視します．したがって，レイノルズ数，粒子径，質量密度，粒子数がパラメータで，本現象は4つの無次元数（
，
，
，
）に支配されます．本研究では，密度比
に代わって，粒子のストークス数
を用いて結果を整理します．ここで，
は粒子の速度緩和時間で，
は乱流中の大きな渦の時間スケールを表します．つまり，
1 のとき粒子は大きな渦によく追従し，
1 のとき粒子は大きな渦にさえ追従できず，粒子と流体に有意な速度差が生まれます．本研究では，
－
の範囲における粒子を調べます．
3. 結果
動画1に，
，
，
の場合における乱流場と粒子の運動の様子を示します．赤色の物体は，速度勾配テンソルの第二不変量の等値面を用いて同定した乱流中の最も小さな渦です．一方，動画2は，同じレイノルズ数および粒子径で，ストークス数を
に変えた場合の結果を示します．これらを比べると，
の（重い）粒子を添加した場合には，粒子の周りにドーナツ状の渦輪が見られます．これは，（粒子径が同じ場合）重い粒子ほど流れの変化に鈍くなるので，主流に対する粒子の相対速度が大きくなり，粒子径程度の渦が剥離するからです．また，
の粒子の方が，壁近くの秩序構造として知られる流れ方向を向いた管状の渦，いわゆる縦渦があまり見られなくなることにも気付きます．（ここで示すようなレイノルズ数が十分に高くない場合には）縦渦が乱流エネルギーをほとんど保有しているので，動画2に示す場合の方が乱流エネルギーはよく低減します．
動画1．
，
，
の場合における可視化．赤色の物体は，速度勾配テンソルの第二不変量の正の等値面を用いて同定した渦で，白色の球が粒子を表します．
動画2．
，
，
の場合における可視化．赤色の物体は，速度勾配テンソルの第二不変量の正の等値面（動画1と同じ値）を用いて同定した渦で，白色の球が粒子を表します．動画1と比べ，壁近くの縦渦が減り，代わりに，粒子の周りに渦が剥離する様子が見られます．
このことは，我々が調べた
種類すべての場合に当てはまります．その証拠に，各粒子によって変調した後の（系全体で平均した）乱流エネルギー
を，粒子を添加していない場合の乱流エネルギーの平均
で除した値を図1に示すと，
が大きいほど，
が
より小さくなることがわかります．つまり，乱流がよく低減します．しかし，乱流の低減率は，
のみでは決まらないこともわかります．
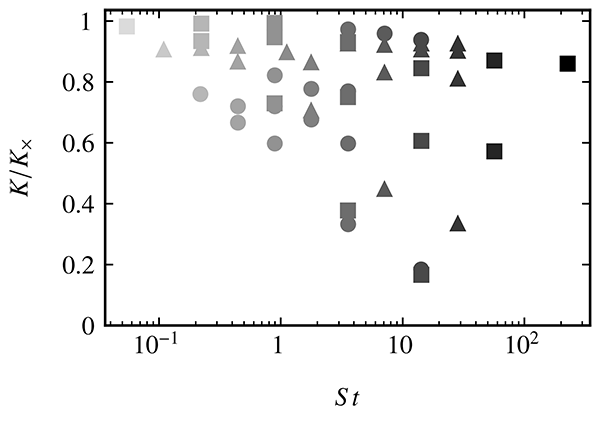
図1．乱流低減率．粒子を添加していない場合における乱流エネルギーの系全体の平均
で規格化した，粒子を添加した場合の乱流エネルギーの平均
を示します．丸が
，三角が
，四角が
の結果で，異なる色は
の違いを示します（つまり，横軸に対応します）．
このように，粒子による乱流低減は，平均流から縦渦に伝達されるはずであった乱流エネルギーを，粒子がバイパスして散逸させることによって起こると考えられます．言い換えると，（粒子を添加しない場合の）平均流による乱流エネルギー生成率
を，粒子を添加したことによる散逸の分
だけ減らすので，粒子を添加した場合の乱流エネルギー生成率が減り，結果として，それと釣り合う乱流エネルギー散逸率
も小さくなります．すなわち，
が成り立つと仮定できます．この仮定と，系全体のエネルギー散逸率から乱流エネルギーを見積もれるという仮定を用いると，乱流エネルギーの低減率を見積もる式
が得られます．詳細な導出方法は，（壁乱流における非一様性には注意が必要ですが）壁のない乱流における変調現象を調べた我々の研究(6)とほぼ同様です．
および
がそれぞれ粒子を添加していない場合における乱流エネルギーとその生成率であることに注意すれば，
より，粒子の添加によって低減した乱流エネルギー
は，粒子によるエネルギー散逸率
で決まると考えられます．
を数値的に評価し，
の左辺を右辺の関数として図2に示すと，確かに，粒子の種類やレイノルズ数によらずに，
が成り立つことが確かめられます．
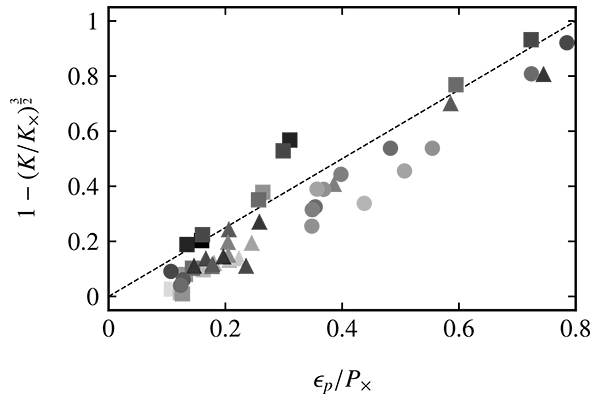
図2．乱流エネルギーの低減率を記述する式
の妥当性の検証．記号は図1と同じ．破線は
を示します．
が粒子の種類やレイノルズ数によらずに成り立つことがわかります．
まとめると，粒子による壁乱流の低減は，「平均流から縦渦に伝達されるはずであったエネルギーを粒子がバイパスして散逸させる」という物理機構で起こります．さらに，これに基づいたいくつかの仮定を用いることで，乱流エネルギーの低減率を記述する式
を提案しました．
4. 結言
固体粒子による壁乱流の低減現象を明らかにするために，粒子のパラメータを系統的に変えて，乱流と粒子の連成数値シミュレーションを実行しました．平板間距離の半幅より十分に小さい粒子を添加すると，系全体の乱流エネルギーはよく低減します．とくに，
が大きいほど，流体と粒子の相対速度が大きくなるので，粒子の周りでのエネルギー散逸が大きくなります（動画1，2）．これに伴い，平均流からの縦渦へのエネルギー伝達が阻害され，その分，乱流エネルギーが減ります（図1）．この乱流低減の物理機構に基づいて，乱流低減率を記述する式を提案しました（図2）．
なお，レイノルズ数がより高くなると，大小さまざまな渦の階層が現れる(7)ので，本研究で考えた平均流によるエネルギー伝達を粒子がバイパスする分に加えて，最大渦からのエネルギーカスケードを粒子がバイパスして散逸する分を考慮する必要があります．
謝辞
本研究の一部は，JSPS科研費（20H02068，21K20403）の助成を受けました．また，理化学研究所のスーパーコンピュータ「富岳」利用課題（hp210207，hp220232）による計算資源の提供を受け，数値シミュレーションを実施しました．また，数値解析の一部は，核融合科学研究所一般共同研究（NIFS22KISS010）の援助のもと行いました．