流れ 2007年4月号 目次
― 特別寄稿 ―
― 特集: 自動車と流れ ―
| リンク一覧にもどる | |
自動車用流体機械における流れの数値解析
|
|
1. はじめに
自動車には,エンジン,自動変速機,ブレーキ,パワーステアリング等の多くの流体機械が用いられている.近年,流体機械の開発においては,機器の性能予測,あるいは性能改善のための知見を得るために数値流体力学 (CFD , Computational Fluid Dynamics) を用いることが多い.自動車用流体機械では狭いすきま内の流れを対象にすることが多く,場合によってはキャビテーションや自由表面を考慮する必要があるため,対象に応じて適切な計算手法や計算モデルの選定,あるいはそれらの開発が必要となる.
本稿では,自動車用流体機械を対象に当社で実施した流れの数値解析の中から代表的な3つの事例についてその概要を紹介する.
スプール弁は流量や圧力の制御用として油圧機器に広く用いられている.スプール弁内部を流体が通過する際にはスプールに流体力が作用する.流体力の半径方向成分である横力は,弁内流れおよびすきまの流れにより生じる圧力の周方向不均一によるものであり,流体固着現象を引き起こすことがあるため,横力を低減する弁の設計が必要である.しかし,弁内流れによる横力に関する研究例は極めて少なく,発生状況や発生メカニズム等の知見はほとんど得られていない.そこで弁内流れの数値解析,可視化実験および圧力計測を実施し,横力の発生メカニズム,および横力に対する弁諸元の影響を検討した.
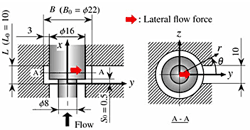
本研究では,高次風上差分を用いた擬似直接解法により弁内の三次元非定常非圧縮粘性流れの数値解を求めた. 図1に対象としたスプー ル弁の構成を示す.計算領域は対称面片側の流路とし,図2のように三つの領域に分けて 400000 ~ 800000 点の格子を生成した.
 |
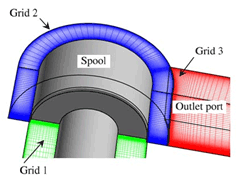 |
| 図1 スプール弁の構成 | 図2 計算格子 |
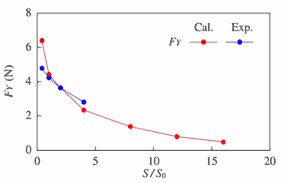
図3にスプール基準諸元における横力 F y を,図4に可視化写真と計算により求めた流脈線を比較した結果の一例を示す. 弁開度が小さい場合において計算と実験の横力に若干の差が認められるが,計算は弁開度に対する横力の変化の傾向をほぼ捉えている.弁内の流れパターンに関しても,噴流の剥離や衝突等の様相が実験と計算で概ね一致している.
 |
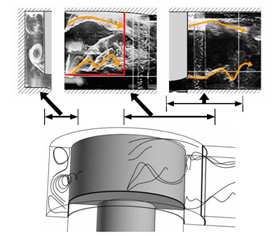 |
| 図3 弁開度に対する横力の変化 ( 基準諸元 ) | 図4 流れパターン ( 基準諸元, S / S 0 =4) |
図5に時間平均速度分布および圧力分布の一例を示す.横力が正方向に作用する理由は次のように説明できる.すなわち,流出ポートを除く断面 [ 図5 (a),(b)] の流れは流入側から流出側へ回り込み,流出ポートへ流出するが,その周方向速度は流出ポート側ほど大きい.圧力は流れの下流側である流出ポート側ほど低いが,周方向速度の増大により流出ポート側ほどさらに圧力が低下するため,図1中赤色の矢印で示した流出ポート ( 正方向 ) に横力が作用する.
横力に対する要因解析結果の一例として,図6にボディ径 B ( B 0 = φ 22) およびスプール軸長 L ( L 0 =10) の影響を示す.いずれの開度においてもボディ径の減少とともに横力は大きくなっている.スプール軸長については,開度により傾向が若干異なるが, L / L 0 が小さい場合に横力が大きい.これらの結果を踏まえ,最終的に横力の低減法を得ることができた.
なお,横力発生メカニズムおよび横力低減法の詳細は文献 (3)を参照されたい.
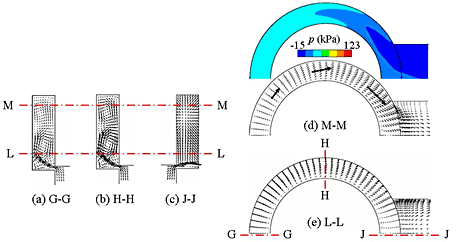
図5 速度分布と圧力分布 ( S / S 0 =1)
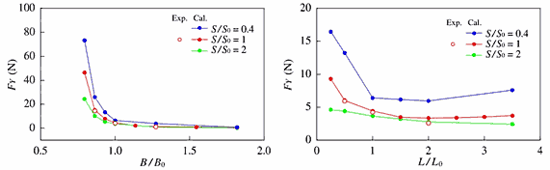
図6 横力に及ぼす諸元の影響
3. ポペット弁のキャビテーション流れ解析 (4) - (5)
自動車用油圧機器の圧力制御に多く用いられるポペット弁には高い制御性が求められるが,その弁特性は背圧によって大きく変化することが知られている.この原因はキャビテーション ( エアレーション ) の発生にあると推測されているが,これまでに確認はされていない.そこで自動車用の作動油を用いた油圧制御用ポペット弁を対象に実験と計算を行い,キャビテーションの発生状況,およびそれに伴う弁特性の変化を調査した.
混相流モデルとしては,油圧機器において特徴的なガス泡 ( 非凝縮性気体 ) と液体の混合状態における見かけの圧縮性を考慮できる圧縮性局所均質媒体モデル (6) を採用した.図7に計算に使用したモデルの概略図および絞り近傍での計算格子を示す.実際の計算は中心軸上で対称条件を課した二次元断面に対して行った.格子点数は約 40,000 点である.
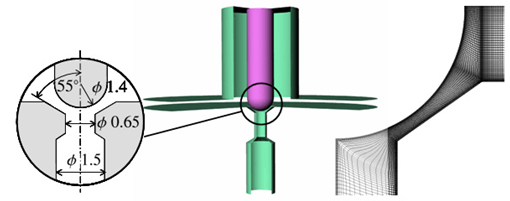
図7 計算用モデルと計算格子
図8に油温 30 ℃でストロボスコープを透過光源として撮影した可視化結果 ( 黒い部分が気相領域,右側は絞り近傍の拡大写真 ) を,図9に油温 70 ℃で連続光を順光源として撮影した可視化結果 ( 白い部分が気相領域 ) を示す.油温の上昇に伴って気泡の発生量が著しく増加していることが分かる.図10は油温 70 ℃(図9に対応)の条件に対して計算で得られたボイド率の瞬間分布を示したものである.絞り近傍での気泡形成,ならびに絞り下流での気泡雲の様子は概ね計算によっても捉えられている .
 |
 |
| 図8 可視化結果 ( Pi = 4MPa , Po = 0.1MPa ,油温 30 ℃ ) |
図9 可視化結果 ( Pi = 4MPa , Po = 0.1MPa ,油温 70 ℃ ) |
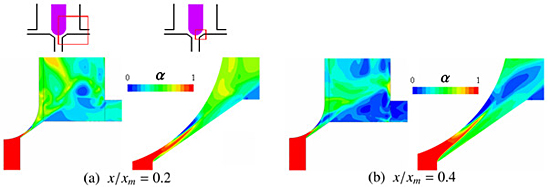
図10 ボイド率分布 ( Pi = 4MPa , Po = 0.1MPa ,油温 70 ℃ )
図11に弁開度に対する流量係数およびポペットに作用する流体力の変化を背圧の異なる 2 ケースについて示す(絞り差圧一定). 低背圧条件(背圧 0.1MPa )での流量係数は大局的に高背圧条件(背圧 9.9MPa )でのそれよりも小さな値を示し,ポペットに作用する流体力は,高背圧条件では弁開度の広い範囲において負の方向(弁を閉じる方向)に作用するのに対して,低背圧条件では常に正の方向に作用する.圧縮性スキームを用いるためキャビテーションが発生していない状態(高背圧条件)では予測精度が低下するが,弁開度に対する流量係数および流体力の変化の傾向は計算によってほぼ捉えられており,背圧によって流量係数および流体力が異なるのはともにキャビテーションの発生が原因であることが明らかにされた.
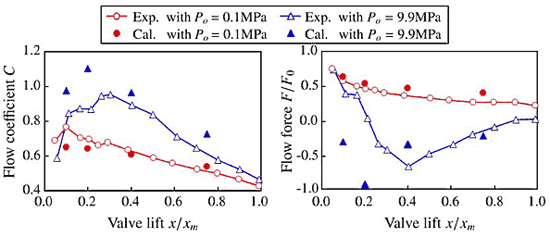
図11 流量係数と流体力 ( 油温 70 ℃ )
4. 燃料噴射弁内流れからのエンジン筒内混合気形成予測法 (7) - (8)
欧州市場を中心にディーゼル機関の低エミッション化,高出力化への開発競争が激化しており,エンジン開発へ貢献できる CFD 技術が必須となりつつある.エンジン筒内混合気形成の数値計算には信頼できる噴霧計算モデルが不可欠である.噴射弁の噴孔出口で噴孔径と同一サイズの均一な液滴を入射する従来の離散液滴モデル (DDM) では,ノズル内の流れ分布やキャビテーションの影響が直接反映されず,噴霧長や混合気形状が実験結果を十分再現できない,あるいはその都度合わせ込む必要があった.そこで本研究では個別の実験値を必要としない普遍性の高い特性予測法を確立するために,ノズル内流れから筒内噴霧・混合気形成までの一貫した計算手法を構築・評価した.
図12にノズル先端部の概形および計算格子 ( 約 13 万セル ) を示す.計算は AVL 社製 CFD コード FIRE ver.8 に改良を加え,次の手順で実施した.まず,オイラー三流体 ( 液相,燃料蒸気相,空気相 ) モデルにキャビテーションモデルを組み合わせてノズル内の非定常流れを計算し,噴孔出口断面での速度,乱れ,空隙率等の分布を設定した時間間隔 ( 今回は 1 ° C.A.) で出力する.次に,それを境界条件として筒内での液柱の分裂挙動を1次分裂モデルで計算し,その後の液滴挙動を DDM により計算する.2次分裂モデルには WAVE モデルを用いた.
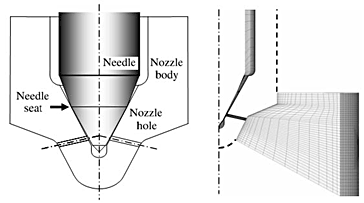
図12 供試ノズルの構成と計算格子
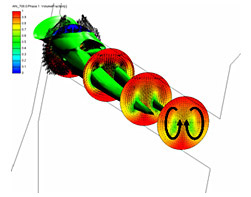
図13にノズル内流れ計算結果を示す.開弁直後の低リフト時には噴孔入口上部で生じたキャビテーションは,左右一対の双子渦 (2次流れ ) によって左右に分離されて噴孔出口まで運ばれる.また,ニードル弁のリフト量によって双子渦の形成位置と回転の向きが変化する様子が捉えられている.
 |
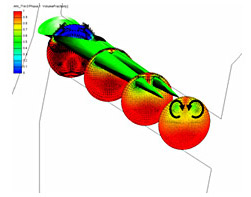 |
| (a) 低リフト ( 開弁直後 ) | (b) フルリフト |
| 図13 ノズル噴孔内の速度分布とボイド率分布 | |
図14に定容容器内の噴霧写真と計算結果,およびペネトレーションの時間履歴を示す.予測された噴霧特性は実験の中実噴霧と 10% 程度の誤差で一致した.
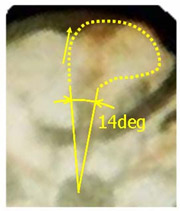
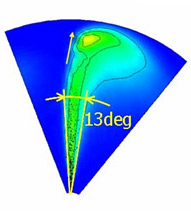
計算結果と筒内観察結果の比較を図15に示す.筒内の噴霧はその先端がキャビティ壁面まで直進し,且つ混合気がスワール方向へ広く分布する.均一な液滴を入射する従来法ではこの二つの特徴の同時再現が困難であったが,本手法では可能となった.その要因は,噴孔出口での流れ分布と一次分裂モデルから計算される不均一な粒径・流速を持った液滴により,半径方向への噴霧の直進性とスワール方向への混合気への広がりが同時に再現されたためである.
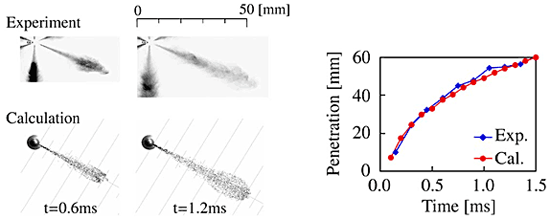
図14 噴霧形状とペネトレーションの時間履歴
 |
 |
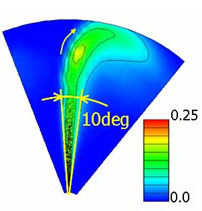 |
| (a) 実験結果 | (b) 本計算結果 | (c) 従来モデル計算結果実験結果 |
| 図15 筒内の噴霧と混合気 | ||
5. おわりに
本稿では,自動車用流体機械を対象に当社で実施した流れの数値解析の中から代表的な3つの事例についてその概要を紹介した.今後,予測精度の向上を図るとともに,さらに複雑な流れ場に対して CFD を適用していく予定である.
参考文献


