という手法が採られている ^(3)(9)(10) ．

　従って，信頼性の高い空力騒音解析を行うためには，第一に，空気流の時間変動を可能な限り精度良く捉えることが重要となる．以下，第 2.1 節では，この非定常流れの高精度な計算を実現するために開発してきた数値計算手法，モデリング技術について説明する．第 3.1 節で述べる風切り音解析では，その計算結果から得られる壁面圧力変動レベルを風切り音の代用評価値としている．

　また，第 2.2 節では，第 3.2 節で述べるウィンドスロッブ現象を予測するために，独自に開発した物理モデルについて説明する．この解法では，流体共鳴音の音圧変動を直接得ることができ，一種の直接解法と言える．第 2.3 節では，分離音場方程式に基づく音場の予測手法を紹介し，その適用例を第 3.3. 節に示した．

2.1 ． 独自の SGS モデルによる LES

　空力騒音などの非定常乱流場の高精度な解析手法として，従来より期待されている手法に Large Eddy Simulation (LES) がある．これは，簡単に言えば，計算格子で解像し得る渦構造を Grid-scale (GS) 成分として直接計算し，格子サイズより小さい渦を Subgrid-scale (SGS) 成分としてモデル化する手法である．（詳細に関しては，例えば文献 ⁽¹⁾⁽²⁾ などを参照されたい．）

　筆者の一部は， GS 成分を計算するための離散化スキーム「改良型コロケーション格子法 ⁽⁴⁾ 」と， SGS 成分の乱流モデル「混合時間スケール SGS モデル（以下 MTS モデル） ⁽⁵⁾⁽⁶⁾ 」をそれぞれ提案している．そして，この両者により，自動車関連の実問題に適用し得る計算精度と実用性を両立させることが可能となった．

　実問題への適用を念頭におき，我々は物体表面に添わせた境界適合型の構造格子を複数組み合わせる重合格子を用いた計算手法を採用している ⁽¹⁴⁾ ．コロケーション格子法 (Collocated grid system) とは，このような計算格子上で，圧力場が空間的に振動するという問題を回避し，また，物理量の保存性を高くする手法である．さらに，文献 ⁽⁴⁾ では，スタガード格子と比べて精度が低下するコロケーション格子の問題点，および運動エネルギーの保存性を改善するための改良を加えている．これにより，誤差要因となる数値粘性を用いなくても実問題に対する安定な計算が可能となった．

　一方， SGS モデルに関しては，従来より， Smagorinsky モデル ⁽¹²⁾ が一般的に用いられている．しかし，このモデルでは，対象とする流れ場ごとに，モデル係数とダンピング関数をチューニングする必要があった．また， Dynamic Smagorinsky モデルでは，モデル係数を自動的に算出してくれるが，計算安定性の問題や予測精度の不十分さが多く指摘されており，実用上必ずしも十分とは言えない．これに対し， MTS モデルは，混合時間スケールを導入することによって，モデル係数を固定したままでも様々な流れ場を高精度に予測することが可能となっており，ダンピング関数は不要である．

2.2 ． 弱圧縮性流体モデル

　自動車まわりの流れは，いかに高速で走行していようとも高々 Mach 数 0.1 程度であり，一般に非圧縮性として扱わる．しかしながら，空力騒音の一つとして重要なウィンドスロッブ現象（後述）はヘルムホルツ共鳴に起因しており，微弱ながらも密度変動を伴うことから，非圧縮性流れを仮定したままの計算では，現象を捉えることができない．

　そこで，著者の一部は低 Mach 数の流れ場における微弱な圧縮性をモデル化し，これを非圧縮性流れの基礎方程式に対する付加項として表現した方程式を導出した ⁽⁷⁾⁽⁸⁾ ．詳細についてはこれらの文献を参照して頂きたい．

2.3 ． 分離音場方程式による計算

　共鳴が発生し，音によって流れ場が変化する場合には，前述の弱圧縮性流体モデルのように圧縮性を考慮した方程式を用いる必要がある．ただし，低 Mach 数の流れ場においては，音が流れ場に大きな影響を及ぼさない場合も多く，この場合には，非圧縮性流れ場と音場を別々に計算する方法（分離解法）が有効であるとされている．特に， Lighthill 方程式 ⁽¹⁵⁾ より，観測点が遠方であると仮定して導いた近似解がしばしば用いられる．ただし，この近似解では，大きな壁面が存在する場合や，音の発生に関わる物体近傍の現象を捉える場合には有効でない．そこで，より正確に音場を扱う方法として，分離音場方程式を用いる方法 ^(16)(17) が提案されている．流れの変動に比べて非常に小さい音の変量を別に計算するため，誤差が小さい．また，流れ場と音場で各々に適した計算方法と計算格子を用いることができる．著者の一部は，この分離音場方程式を用いた解析手法を，後に示す事例に適用した．この事例で，応用問題においても，音の発生・伝播を捉えることができ，音場計算が有効であることを示した．

３． 計算事例

3.1 ． 風切り音解析

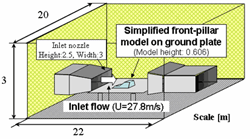
　フロントピラーで発生する風切り音の低減は，自動車にとって最も重要な課題の一つである．ここでは，図 1 に示す基礎的な実験模型に対して， MTS モデルによる LES を用いて，見かけ上の音源であるサイドウィンドウ上の圧力変動を予測した例を示す．併せて，従来用いていた擬似直接解法 ⁽¹⁴⁾ による計算結果も載せる．疑似直接解法（QUICK 法）とは， LES の SGS モデルを高次精度風上差分による数値粘性で代用した手法と言えるが，乱流の挙動を再現するための物理的な裏付けはないため，特に非定常性の強い流れ場の計算精度が不十分であると考えられる．

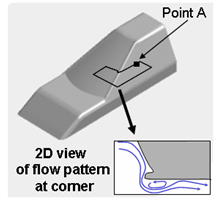
　図 2 に，図 1 中に記した再付着点近くの計測点 A における壁面圧力変動の周波数スペクトルを示す．計算格子に対する依存性を確認するために，解像度の異なる 3 種類の格子で計算している．実験結果をみると，ここでの圧力変動は，特定の周波数でピークを持つことなく，高周波数までの広帯域な変動スペクトルを持つことがわかる．

　擬似直接解法に比べ， LES の方がより高い周波数帯まで実験に近い結果を示していることがわかる．実験に一致している周波数の上限は，最も高い解像度の格子の場合でおよそ 2kHz であるが，このあたりの周波数まで予測できれば，車両の設計・開発に際して十分に有用な情報を与えられる．

(a) 風洞実験の全体図 （流入速度 : 27.8m/s ）	(b) 基礎実験模型と角部での流れパターン （模型高さ : 0.606m ）
図 1 フロントピラー風切り音基礎実験模型

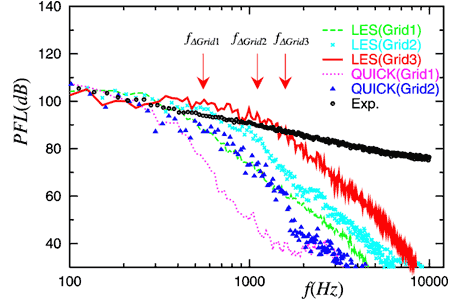
図 2 サイドウィンドウ上の圧力変動スペクトル
LES: MTS モデルを用いた LES の結果， QUICK: 擬似直接解法の結果， Exp.: 実験結果，
Grid1,2,3: 計算格子の解像度の違い (Grid1 が最も粗く， Grid3 が最も細かい )
f_ΔGrid1,2,3: 各格子で予測し得る限界周波数の推定値

3.2 ． ウィンドスロッブ解析

　ウィンドスロッブとは，自動車のサンルーフやサイドウィンドウを開けて走行する場合に車室内に発生する耳を圧迫するような低周波数（10 ～ 50Hz 程度）の騒音である．これは車室が共鳴箱の役目を果たして発生するヘルムホルツ共鳴音の一種である．

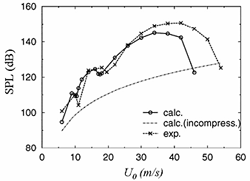
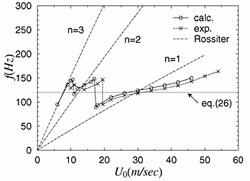
　ここでは，図 3 の基礎実験模型に対する結果を示す．この模型は上面に穴の開いた直方体の箱（3 次元オープンキャビティ）でサンルーフ開口時の車室内を模擬している．図 4, 5 が上面の流速 U を変えた時の音圧レベル SPL と共鳴周波数 f の変化を表したグラフである．

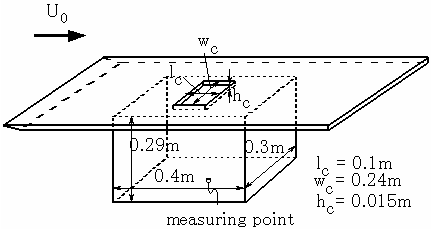
図 3　　3 次元オープンキャビティ実験模型
U 0 : 上面の流れの速度（5m/s から 55m/s まで変化させる），
measuring point: 音圧計測点

図 4 音圧レベルの変化 calc.(incompress): 通常の非圧縮性流体解析による結果， calc.: 弱圧縮性流体モデルによる計算結果， exp.: 実験結果	図 5 周波数の変化 calc.: 弱圧縮性流体モデルによる計算結果， exp.: 実験結果， Rossiter: 共鳴の各モード (n=1,2,3) に対応する Rossiter による実験式 (11) の値

　図 4 から，数箇所の特定の流速で音圧レベルが極大値をとるというウィンドスロッブ特有の現象が計算 (calc.) によっても，実験 (exp.) と同様に捉えられていることがわかる．一方，図中の一点鎖線は非圧縮性流れの計算手法で得られた結果であるが，これではそのような現象は全く再現できない．

　図 5 からは，流速に対する周波数特性が計算と実験でよく一致している様子がわかる．ヘルムホルツ共鳴の影響により渦放出の周波数のモード（図中に示した n =1, 2, 3 の一点鎖線）が変わるときに，図のような不連続な変化が発生すると考えられる．また，図中の細い実線は模型の開口部面積やキャビティ容積などから推定されるヘルムホルツ共鳴周波数の予測値であるが，流速 30m/s 前後では，ウィンドスロッブ音の周波数が幅広い範囲でヘルムホルツ共鳴周波数にロックインされる現象も捉えられている．

3.3 ． 分離音場方程式による音場解析

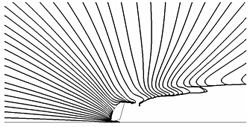
　ドアミラーから発生する風切り音の解析例 ⁽¹⁸⁾ を図６に示す．形状を単純化したドアミラーを平板に設置し，一様流中に置いた場合を計算した．図のように，３次元的な音場の解析が可能であり，発生原因箇所や，平板に沿って伝わる音の音圧分布などを調べることが可能になった．また，音響インテンシティベクトルの空間分布を求めることが可能であり，図７のような音響インテンシティベクトルによる流線（音響流線）を描画することができる．さらに，図のように，各周波数帯における伝播特性も示すことができる．実験では，しばしば音響インテンシティベクトルを計測して音の発生箇所を探査する．図の計算結果は，実験では捉えがたい物体近傍までの様子を示しており，観測結果の解釈に役立つものと考えられる．

図６ ドアミラーから発生する風切り音の音圧分布（ある瞬時の様子）．
平板上の分布とドアミラー中央付近の断面の分布（半透明）．

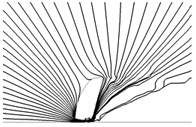(a) 全周波数帯の音による音響流線．	(b)1kHz から 2kHz 帯の音による音響流線（拡大図）．
図７ 音響流線（流れに垂直かつ平板に平行な方向から見た様子）．

４． むすび

　筆者の周辺で実施している空力騒音解析の現状に関して，その解析手法と事例を述べてきた．非定常流れ場の高精度な予測と，流体共鳴現象の予測については，概ね満足し得る結果が得られるようになってきたが，実用性の更なる向上のためには，

• 計算時間の更なる短縮
• 広帯域音へ適用し得る汎用的な騒音予測手法の進展
• 音の伝播・透過（車外で発生している騒音が車室内でどのように聞こえるか）のモデル化

といった技術課題の解決が望まれる．

参考文献