近年，自動車の高速化や高性能化が進み，環境問題対応や快適性向上の必要性が高まる中，車両周り流れの制御や空力特性の向上が重用視されてきている．また，自動車においては，車両周り流れに留まらずエンジンの燃焼や駆動系のオイル流れ，ブレーキ冷却風流れ，エンジンルーム内の冷却風流れ，室内の空調流れ等，様々な流れが関係しており流体力学は無くてはならないものとなっている．近年，数値流体力学 ( CFD: Computational Fluid Dynamics ) の目ざましい発展に伴い， CFD は自動車設計において種々の流れを予測，理解するために必要不可欠なツールになりつつある．

　車両の空力設計における実用計算では， RaNS(Reynolds averaged Navier Stokes) 型乱流モデルを用いた定常解析が多く用いられているのが現状である．計算手法としては，差分法や有限要素法，有限体積法にもとづく領域型解法が一般に多く用いられているが , これらの手法により解析を実施するためには計算格子の生成は必要不可欠であり , 計算格子の生成に非常に手間がかかることが大きな課題となっており，複雑な車両形状への CFD 応用の実用性を重視するため格子生成手法の開発に力が注がれてきた．一方で流体騒音や車両の走行安定性を予測するツールとして非定常解析への要求も高まっており LES(Large eddy simulation) を含む高度モデルを適用した非定常解析についても報告されている ^{(1), (2)} ．

　著者らのグループでは，既存の CFD とは異なる視点で自動車周りの非定常流れを手軽に解析することができる CFD ツールの開発を進めており，既存の CFD 解析手法が抱えている格子生成の困難さを根本的に回避する方法としてメッシュレス手法の一つである渦法に注目した．渦法は，積分方程式に基づいた解析法であるため，流れ場に計算格子の形成を必要とせず，車両のような複雑形状ならびに 移動･変形境界 を容易に取り扱うことができ，且つ空間の渦度分布を離散的にモデル化し個々の離散要素の挙動をラグランジュ的に追従することにより流れを表現する手法であることから，基本的に RaNS 型の乱流モデルを必要としないといった特徴がある．最近では，渦法の乱流への適応性を示した先進的な研究成果 ^{(3), (4)} や車両周りの流れ解析に適用した結果 ^{(5), (6)} が報告されている．以下では，渦法を用いて重量車両周りの非定常流れ解析を行った結果 ⁽⁷⁾ を紹介する．

２． 重量車両の空力への応用

　重量車両モデルとして， Gutierrez ら ⁽⁸⁾ が実験に使用した Ground Transportation System (GTS) モデル ( 図 1) について解析を実施した． GTS モデルにおいて，トレーラーに作用する抗力は，トラクターとトレーラーの隙間長さによって劇的に変化することが過去の実験的研究 ⁽⁹⁾ より知られている．隙間長さの変化によるトレーラー抗力の変化の再現性について検証するために， 2 種類の隙間長さ ( G / S 1/2 =0.25 ， 0.65 ) について解析を実施し実験結果と比較した．ここで， S はトラクターの前方投影面積である．計算は，前方投影面積 S および車両走行速度 U 0 を用いて無次元化したレイノルズ数 Re= U 0 S 1/2 / n = 3.0 × 10 6 に対して実施した．

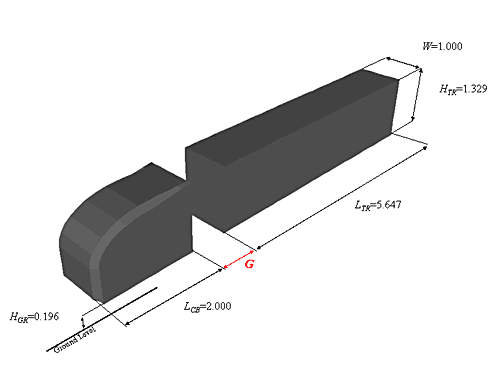
図 1 GTS モデル

 

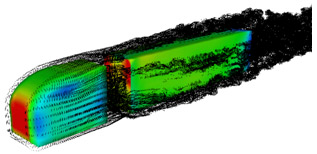
　図 2 には，異なる隙間長さのトラクター・トレーラー周りの流れの様子を渦要素分布および物体表面の圧力分布を用いて示す．それぞれの図において，トラクターのフロントピラー付近から流れ出した渦要素が，流下するにしたがいトレーラー側面で縦渦を形成している様子が確認できる．また，トレーラー側面下部では，地面と床下の隙間から渦が巻き上がっている様子が確認できる．隙間長さが大きいとき，前方のトラクターによって形成された後流は，トレーラー前面に衝突し，隙間内に流れ込むことによりトラクターとトレーラーの隙間には，非常に複雑な渦流れが形成されるものと考えられる．図 3 には，車両隙間の中央高さ断面内における速度および渦度の分布を示す．隙間長さが小さいとき，対称な渦度分布となっているのに対し，隙間長さが大きいときは，非対称な渦構造が形成されていることが分かる．隙間長さが長いときに隙間内に形成された非対称な渦は不安定であり，時間的に揺動することにより車両に大きな変動力が作用すると考えられる．

 

(a) G/S1/2 =0.25
(b) G/S1/2 =0.65
図 2 　重量車両周りの渦要素分布図 （図をクリックすると動画が再生されます。QuickTime形式 各々11MB）

 

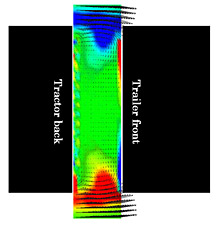(a) G/S1/2 =0.25

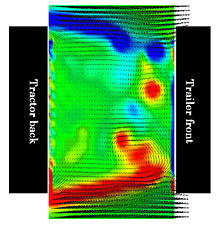(b) G/S1/2 =0.65

図 3 　車両隙間の渦度分布

 

　図 4 には，トラクターおよびトレーラーに作用する抗力に対する隙間長さの影響について実験と比較した結果を示す．図中のエラーバーは，抗力の最大値および最小値を表す．隙間長さが長いとき，隙間が狭い場合に比べてトレーラーに作用する平均抗力が大きくなると共に，変動の振幅も大きくなっていることが確認でき，実験と同様の傾向が捉えられていることが確認できる．

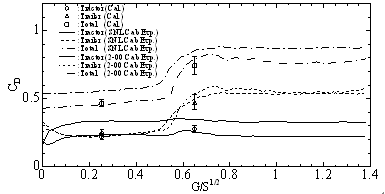
図 4 　車両隙間長さに対する抗力係数

 

３． 蛇行する車両まわりの流れ

　走行中の車両は，幾度となく姿勢を変えることがあり，その度に車両周りには非常に複雑な流れ現象が発生すると考えられる．しかし，このような流れは実験により調査することも困難である．そこで，本解析手法の応用として蛇行する車両についての解析を実施した．図 5 には，蛇行する車両周りの流れの様子を渦要素分布を用いて示す．トラクターにより生成された後流とトレーラーとの干渉により後流には非常に複雑な渦流れが形成されることが分かる．

図 5 　蛇行する重量車両周りの渦要素分布図
（図をクリックすると動画が再生されます。QuickTime形式 6MB）

 

　図 6 には，トラクターおよびトレーラーに作用する抗力係数の時間履歴を示す．トラクターおよびトレーラーに作用する抗力は，車両の姿勢に応じて変化していることが確認できる．また，注目すべき点は，トラクターおよびトレーラーの姿勢によってトレーラー抗力が負になる場合があることである．これは，車両が蛇行することによりトラクターとトレーラーの隙間形状が変形し，その影響でトレーラーに推進力が作用したものと考えられる．このように車両が運動中に作用する流体力ならびに流れ現象は極めて複雑であり，コーナリング時や加･減速中の車両の走行安定性を考える上でも興味深いものであると考えられる．

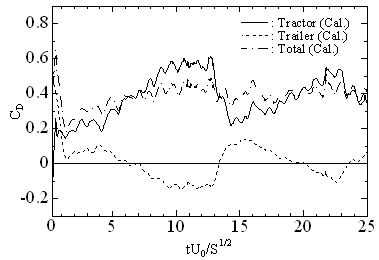
図 6 　蛇行する重量車両に作用する抗力係数

４． おわりに

　本稿では，車両空力解析へのアプローチとして，格子形成が不要，乱流モデルが不要，移動･変形境界が自在という 3 つの特徴をもつ渦法を紹介し，重量車両周りの流れに関する解析例を示した．今後，自動車開発で必要とされる流体解析に加えて 構造や騒音，熱，化学反応などとの様々な要素解析を組み合わせた実用的な連成解析への発展が期待される．

 

参考文献

(1)	谷口 , 他 , 追従自動走行を想定した車両空力の数値解析 , 自動車技術会春季大会 #20015268, 2001.
(2)	鬼頭 , 他 , 車両床下流れの研究 , 自動車技術会春季大会 #20065159, 2006. (1) Cottet, G.H., et al. , A comparison of spectral and vortex methods in three-dimensional incompressible flows, J. Comp. Phys. 175, pp.702-712, 2002.
(3)	Cottet, G.H., et al. , A comparison of spectral and vortex methods in three-dimensional incompressible flows, J. Comp. Phys. 175, pp.702-712, 2002.
(4)	福田　紘大，亀本　喬司 , 渦法による乱流モデル構築に向けたラグランジュ型渦要素再配置モデルの提案 , 日本機械学会論文集 B 70-697, 2004.
(5)	Bernard, P. S., et al., Vortex Method Simulation of Ground Vehicle Aerodynamics, SAE World Congress, Detroit , MI , USA , 2005.
(6)	Daeninck, G., et al., Simulation of Vehicle Aerodynamics Using a Vortex Element Method, United Engineering Foundation Conference on Aerodynamics of Heavy Vehicles, Trucks, Buses, and Trains, CA, USA, 2002.
(7)	Kamemoto, K., Ojima, A., Applicability of the Vortex Methods for Aerodynamics of Heavy Vehicles, United Engineering Foundation Conference on Aerodynamics of Heavy Vehicles, Trucks, Buses, and Trains, CA, USA, 2002.
(8)	McCallen R., et al., Working Group Meeting on Heavy Vehicle Aerodynamic Drag, UCRL-ID-135358, 1999.
(9)	Gutierrez WT, et al., Aerodynamics Overview of the Ground Transportation System (GTS) Project for Heavy Vehicle Drag Reduction. SAE 960906, pp.219-236, 1996.

リンク一覧へ戻る

更新日：2007.4.2