流れ　2008年9月号　目次

 

金属表面における気体分子の解離現象の数値解析

徳増崇 東北大学

1. はじめに

　金属表面上における気体分子の解離吸着現象のメカニズムについての知見を得ることは, 様々な触媒反応を理解する上で極めて重要な課題であり, 現在に至るまで様々なアプローチによる研究が行われてきている. 近年の計算機の発達, 計算アルゴリズムの進歩により, 分子シミュレーションがこのような解離吸着現象の原子レベルでの機構に対する知見を得る上で非常に有効な手法となってきており, 現在では密度汎関数法(Density Functional Theory: DFT)により解離経路や解離障壁の大きさを求め, 遷移状態理論により解離確率を見積もる方法が一般的である. しかしながら, これらの解析は分子の運動状態が解離現象に与える影響を全く考慮しておらず, また近年行われている6-Dポテンシャルによる解離現象の分子動力学計算^{[1, 2]}においても、温度0 Kを仮定して表面原子を固定した状態で行うため, 表面原子の運動状態が解離現象に与える影響を考慮することができず, 得られた解離確率が実験結果と異なる傾向を示すことが指摘されている^[3]. このような金属表面原子と気体分子の相互作用を物理的に考慮して計算を行う手法に原子挿入法(Embedded Atom Method: EAM)がある^[4]. この手法の原理は密度汎関数理論に基づいており, 系の全エネルギーをある電子密度に原子を埋め込む際のエネルギーと原子-原子核間相互作用ポテンシャルエネルギーの和に分割して表現している.この手法を用いて金属表面の熱運動までをも考慮した気体分子の解離吸着現象を解析することができれば, より現実に近い系での知見を得ることが期待でき, かつ複雑な形状をした表面への拡張も容易に行えると考えられる. ここではこのEAMを用いて金属表面の熱運動を考慮した気体分子の解離吸着現象を, 特に解離確率について解析した事例を紹介する. 詳しくは文献^[5]を参照して頂きたい.

 

2. 計算手法

　EAM法において, N個の原子で構成されるPt表面と1つのH₂分子の相互作用ポテンシャルエネルギーE_potは次のように表される.

　　 (1)

ここで, 添え字i,jはPt原子を, 添え字kはH原子を表し, Rは原子間距離である. は周りの原子によって形成される電子密度がrとなる位置に原子を埋め込むときに必要なエネルギーであり, 原子と系全体の電子の相互作用を表す項である. , はそれぞれPt原子, H原子を埋め込むのに必要なエネルギーである. は距離Rの位置にある原子間の2体相互作用ポテンシャルであり, , , はそれぞれPt原子同士間, H原子同士間, PtとH原子間に働く2体相互作用ポテンシャルである. , はそれぞれ周りの原子によってPt原子i, H原子kの位置に形成される電子密度である. EAMではこの, は周りの原子1つ1つからの電子密度の重ね合わせにより近似する. 式(1)の関数系およびパラメータは, 式(1)によって得られる電子状態やポテンシャルがDFTの計算結果をよく再現するように決定されている. 図1にPt表面の各サイトの位置および角度の定義を, 表1に式(1)により計算されたPt-H₂系の解離障壁の位置およびその値を示す. 表1より, 式(1)のポテンシャルは非常によくDFTの計算結果を表していることがわかる.

 

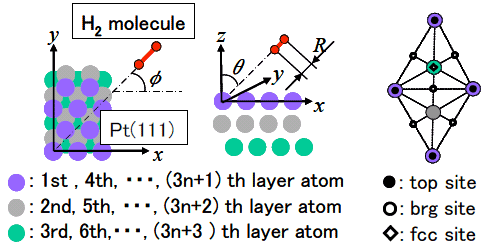
図1: Pt(111)表面における各サイトの位置および角度の定義.
表面第1層の真上がtopサイト, 第3層の真上がfccサイト, 2つのtopサイトの中間がbrgサイトと呼ばれる.

 

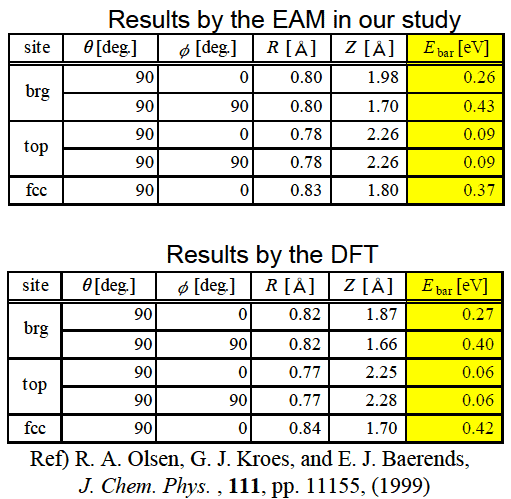
表1: EAMポテンシャルにより得られた解離障壁の値とDFTによる計算結果の比較.
式(1)のEAMポテンシャルにより計算された解離障壁は良い精度でDFTの計算結果と一致していることがわかる.

 

3. Pt-H₂系の解離吸着現象の分子動力学シミュレーション

　 式(1)のポテンシャルを用いて, 白金表面に入射するH₂分子の挙動を分子動力学法により計算し, 解離確率を求めた. 図2に計算系の概略図を示す. Pt(111)面はx方向に10個(27.72Å), y方向に10個(24.00 Å), z方向に3層の計300個の原子で構成されている. x, y方向には周期境界条件を課した. これらの原子の初期配置はPtバルクの結晶構造と同様の位置とした. またPtの格子定数は3.92 Åとした. Pt表面の温度制御はPhantom原子を用いて行った^[6]. Pt表面はH₂分子を入射させる前に温度T [K]の平衡状態が実現されるまで緩和計算を行った. このPt(111)表面に各サイトの高さ5.0 Åの位置からH₂分子を入射させた. H₂分子には初期並進エネルギーe_trと初期回転エネルギーe_rotを与えた. その並進エネルギーは面に垂直で面に近づく方向の速度で与え, 回転エネルギーはH₂分子の結合軸に垂直な１方向の角速度で与えた. またH₂分子の初期位相はランダムに与えた. 時間積分法にはVerletの方法^[7]を用い, 時間刻みはΔt=1.0×10^-16s として計算を行った.

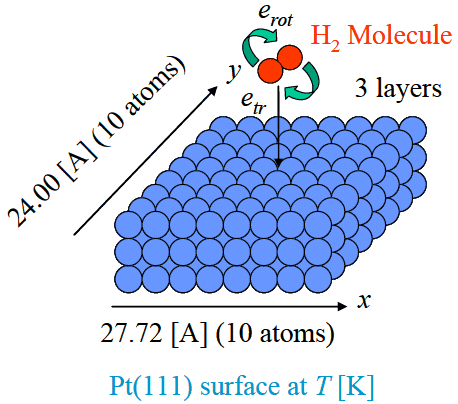
図2: Pt(111)-H₂系の解離吸着シミュレーションの模式図. Pt表面は10×10×3=300個のPt原子によって構成され, Phantom原子を配置することにより温度制御を行っている. その表面に垂直に, 並進エネルギーe_tr, 回転エネルギーe_rotを与えたH₂分子を入射させている.

　 図3に衝突時の分子挙動の例を示す. Case AはH₂分子が解離した例, Case BはH₂分子が解離障壁は乗り越えたものの, Pt表面で解離せずに跳ね返った例を表している. これらは両方とも解離障壁を乗り越えているため従来の遷移状態理論では”解離した”とみなされるパターンであるが, 分子の運動状態を考慮することによりこのような解離障壁を乗り越えても解離しないパターンを”解離した”ケースから分離することができる. このような計算を, 分子の位相を変化させて各並進・回転のエネルギーの組み合わせごとに全部で640回の計算を行い, この640回の計算のうち, 解離したケースを数えることでそのエネルギーにおける解離確率を計算した. ここでは, 水素の原子間距離が3.5 Å 離れたケースを”解離した”と見なした. 図4にその結果の一例を示す. ここで分子の初期回転エネルギーはで一定としている. また, この図でPt-FixとはPt表面を固定したケースを, Pt-Move[T=0 K]はPt表面の温度を0 Kに制御したケースを, Pt-Move[T=300 K]はPt表面の温度を300 Kに制御したケースを表している. 一般的には解離確率は初期並進エネルギーが小さいときは解離障壁を越えられないため0であるが, 初期並進エネルギーの増加に伴い解離障壁を越えられる分子の数が増加するため解離確率は増加する傾向にある. 図4はその傾向をよく表しているが, Pt表面が動いている状態ではその運動状態によって解離障壁が変化するためPt表面が固定された場合に比べてより低い初期並進エネルギーで解離が始まっていることがわかる. また入射H₂分子が解離障壁を越えるのに十分な初期並進エネルギーを持っていても, 図3のCase Bのように解離せずにPt表面で跳ね返ってしまう分子が存在するため, 解離確率は1に漸近していないことがわかる. このように, Pt表面の運動状態, 入射分子の運動状態を考慮することによって, より現実に近い, 詳細な解離現象の解析が可能となる.

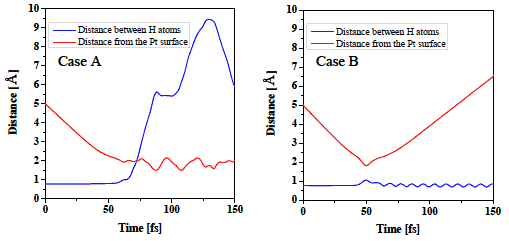
図3: 衝突時のH₂分子の壁面からの距離およびH原子間距離. 図中青線がH原子間距離を, 赤線がH₂分子の表面からの距離を表している. Case A(解離)では衝突時に原子間距離が大きくなり, H₂分子が解離していることがわかる. 一方, Case Bでは解離障壁を乗り越えてPt表面にH₂分子が衝突しているものの, 解離せずにそのまま跳ね返っている様子が観察できる.

 

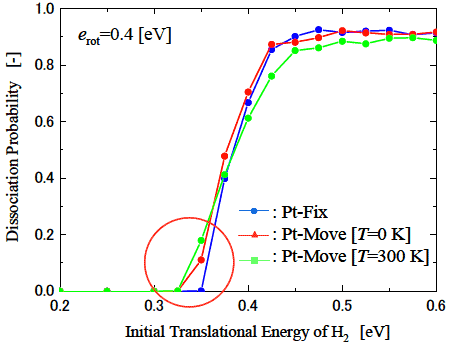
図4: H₂分子の初期並進エネルギーに対する解離確率の変化. Pt表面が300 Kに相当する熱運動をしているケースでは表面が固定されている場合に比べて, より低いエネルギーから解離が起こり始めていることがわかる. また, 入射H₂分子が解離障壁を乗り越えるのに十分なエネルギーを持っていても, 全ての分子が解離するわけではないため, 解離確率は1に漸近していない.

 

4. おわりに

　 本稿では, 金属表面における気体分子の挙動を分子動力学法を用いて計算し, 金属表面を構成する原子や気体分子の挙動が解離確率に与える影響について紹介した. 計算機の発達に伴い, 今後このような分子の化学反応を伴う固体―気体界面の流動現象の数値解析が非常に重要になると思われる. 本稿がその一助となれば幸いである.

参考文献

[1]	Olsen, R. A, Kroes, G. J. and Baerends, E. J., "Atomic and molecular hydrogen interacting with Pt(111)" J. Chem. Phys., Vol. 111, (1999), pp. 11155-11163
[2]	Olsen, R. A., Busnengo, H. F., Salin, A., Somers, M. F., Kroes, G. J. and Baerends, E. J., "Constructing accurate potential energy surfaces for a diatomic molecule interacting with a solid surface: H2+Pt(111) and H2+Cu(100)" J. Chem. Phys., Vol. 116, (2002), pp. 3841-3855
[3]	Vincent, J. K., Olsen, R. A., Kroes G. J. and Baerends, E. J., "Dissociative chemisorption of H${}_{2}$ on Pt(111): isotope effect and effects of the rotational distribution and energy dispersion" Surf. Sci. Vol. 573, (2004), pp. 435-445
[4]	Daw, M. S. and Baskes, M. I., "Embedded-atom method: derivation and application to impurities, surfaces, and other defects in metals" Phys. Rev. B, Vol. 29, No. 12 (1984), pp. 4272-4282
[5]	徳増崇, 原香菜子, 伊藤大吾, “金属表面上の気体分子の解離吸着現象に関する分子動力学的解析” 日本機械学会論文集B編 第74巻739号 (2008), pp.684-691
[6]	Blomer, J. and Beylich, A. E., “MD-Simulation of Inelastic Molecular Collisions with Condensed Matter Surfaces" Proc 20th Int. Symp. on Rarefied Gas Dynamics, (1997), pp. 392-397.
[7]	Allen, M. P. and Tildesley, D. J., Computer Simulation of Liquids, Clarendon Press, Oxford (1986)