流れの読み物

Home > 流れの読み物 > ニュースレター > 2023年10月号

流れ　2023年10月号　目次

―　特集テーマ：ASME-JSME-KSME流体工学国際会議　―

  1. 巻頭言
    （朴，松田，洪）
  2. 横風に対する鉄道車両の耐力評価方法と安全な鉄道運行のためのその応用
    三須 弥生（JR東日本）
  3. 乱流の中の秩序
    後藤 晋（大阪大学），本告 遊太郎（大阪大学）
  4. LES/粒子シミュレーションによる化学反応を伴う乱流平面噴流の数値解析
    シン ジャボオ（名古屋大学）,　渡邉 智昭（名古屋大学大学院）,　長田 孝二（京都大学大学院）
  5. 液体ロケットインデューサにおけるキャビテーション不安定現象発生時の翼端漏れ渦キャビテーションの非定常特性
    田村 浩紀（東北大学），奈倉 悠人（東北大学），川崎 聡（宇宙航空研究開発機構），伊賀 由佳（東北大学）
  6. Water Condensation in PEMFCs at Nano-scale: Insights through Lattice DFT simulations
    Clint John Cortes OTIC（東京大学），Masazumi ARAO（FC-Cubic），Masashi MATSUMOTO（FC-Cubic），Hideto IMAI（FC-Cubic），Ikuya KINEFUCHI（東京大学）
  7. Reconstruction of Fluid Stress Field from Flow Birefringence using Physics-Informed Convolutional Encoder-Decoder (PICED)
    Daichi IGARASHI（東京農工大学），Shun MIYATAKE（東京農工大学），Jingzu YEE（東京農工大学），Yoshiyuki TAGAWA（東京農工大学）
  8. Determination of Permeability in the Volume Penalisation Method with a Smooth Mask Function
    辻元 大智（大阪大学），中尾 祐太（大阪大学），辻 拓也（大阪大学），田中 敏嗣（大阪大学），鷲野 公彰（大阪大学）

 

乱流の中の秩序


後藤 晋，

本告 遊太郎
大阪大学

1.　はじめに

　乱流は文字通り乱れた流れである．しかし，一見したところランダムな流れであっても，慎重に観察すると，秩序立った構造の集合であることが分かる．私たちは，乱流という複雑な現象を，なるべく単純な物理描像で記述できないかと考えてきた．このときに，鍵を握るのが秩序構造である．もっとも，乱流中に秩序構造があることは古くから広く認識されてきたし（１），例えば，台風を気象衛星の画像で観察すれば容易に理解できる．

　ところで，乱流の大規模数値シミュレーションが盛んに行われるようになり，三次元の流速場の詳細な時系列データが得られるようになったことで，秩序構造に対する理解も深まってきた．このニュースレターでは，文献(2-6)で示した，周期箱乱流，円柱後流，および平行平板間乱流中の秩序構造とその維持機構について簡単に紹介する．

２. 秩序渦の階層

　秩序構造の代表は渦である．渦は「渦度が大きい領域」あるいは，「速度勾配テンソルの第二不変量が正の領域」として定義することが多い（文献(1)の2.4節）．ところが，発達した乱流中の渦をこれらの量で同定しようとすると，図1(a, b, c)に示すように，微細な渦の森が見えるばかりである．これは，乱流のエネルギースペクトルの性質から，速度勾配テンソルが乱流中の最小渦により決まるためである．言い換えると，乱流の運動エネルギーは最大渦が保有する一方で，その散逸は最小渦が担うという性質による．つまり，この性質は，よく知られるエネルギーカスケード描像（文献(1)の4.1節を参照）を反映するとも言える．


図１　(a-c) 渦度の大きさ，あるいは速度勾配テンソルの第二不変量の等値面で可視化した微細渦の森．
(d-f) 流れ場をスケール分解することで捉えた秩序渦の階層．
赤色が最大渦，黄色が中渦，青色が小渦を表す．(a, d) 周期箱乱流，(b, e) 円柱後流，(c, f) 平行平板間乱流．

　解析した乱流の一次元縦エネルギースペクトルを図2に示す．とくに，周期箱乱流（テーラー長に基づくレイノルズ数はおよそ250）のエネルギースペクトルには，-5/3乗則が明確に見られる．したがって，この乱流中には渦の階層が存在するはずである．しかし，上述のように，生の速度勾配テンソルを用いる限りは，この階層を捉えることはできない．そこで，スケール分解を行う．周期境界条件下の流れの場合にはフーリエ展開が可能なので，バンドパスフィルタを用いれば容易にスケール分解が可能である．図1(d)にスケール分解後の様子を示す．図1(a)では微細渦のランダムな集合にしか見えなかった乱流中にも明確な秩序渦の階層が存在することが分かる．


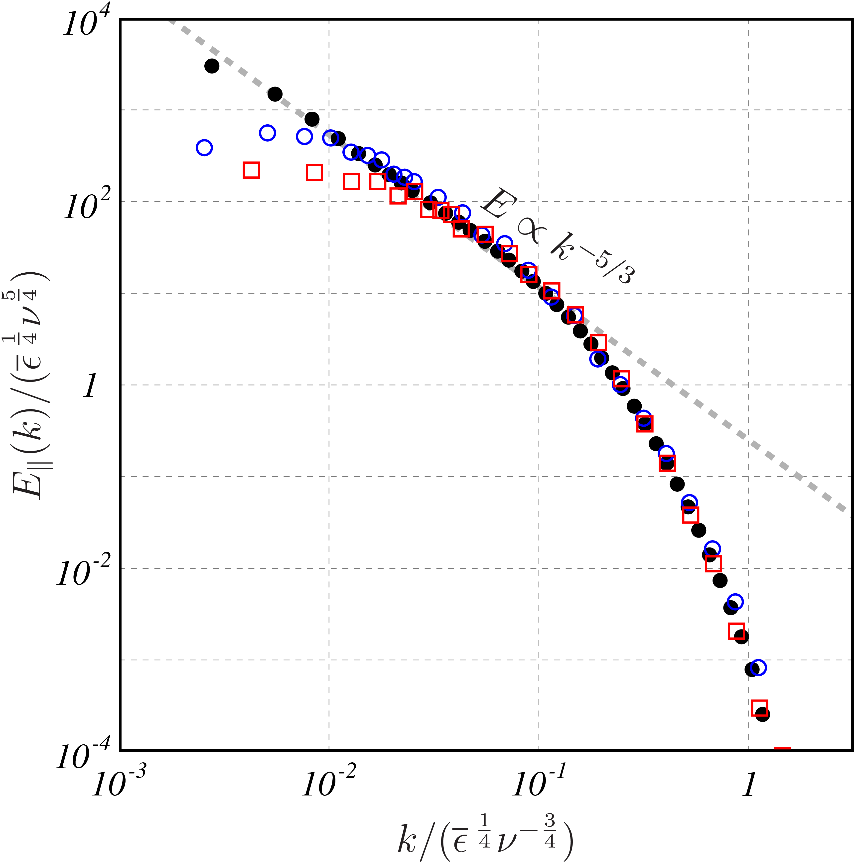
図２：一次元縦エネルギースペクトル．
黒丸が周期箱乱流，青丸が平行平板間乱流，赤四角が円柱後流．詳細は文献(6)を参照のこと．

　一方で，フーリエ分解が使えない円柱後流や平行平板間乱流に対しては，実空間のフィルタ（7）を用いれば同様にスケール分解を行える．結果を図1(e, f)に示す．確かに，これらの乱流中にも明確な渦の階層が認められる．

３. 維持機構

　発達した乱流中の秩序渦の階層が明らかになったので，次にその維持機構について考える．秩序渦の階層の生成機構は，エネルギーカスケードの物理機構にも直結するので，その解明は乱流の動力学や統計を理解する上で重要な問題のひとつである．

　まず，周期箱乱流および円柱後流における異なるスケールの階層の渦を図3(a, b)に示す．これらの図から，「より小さな渦が，より大きな渦の周囲に生成される」ことが分かる．とくに，同じスケールの管状渦は，逆旋回するものどうしが対をなす傾向がみられる．この傾向は，とくに円柱後流中の生まれたての渦で顕著である（図3(b)）．一方で，発達した乱流中ではさまざまな年齢の渦が混在するため，図3(a)のような分かりやすい事例は探し出す必要がある．いずれにしても，逆旋回渦対の周囲には引き伸ばし場が存在するので，その引き伸ばし場でより小さな渦が生成されると考えると，渦の階層の生成機構がよく理解できる．


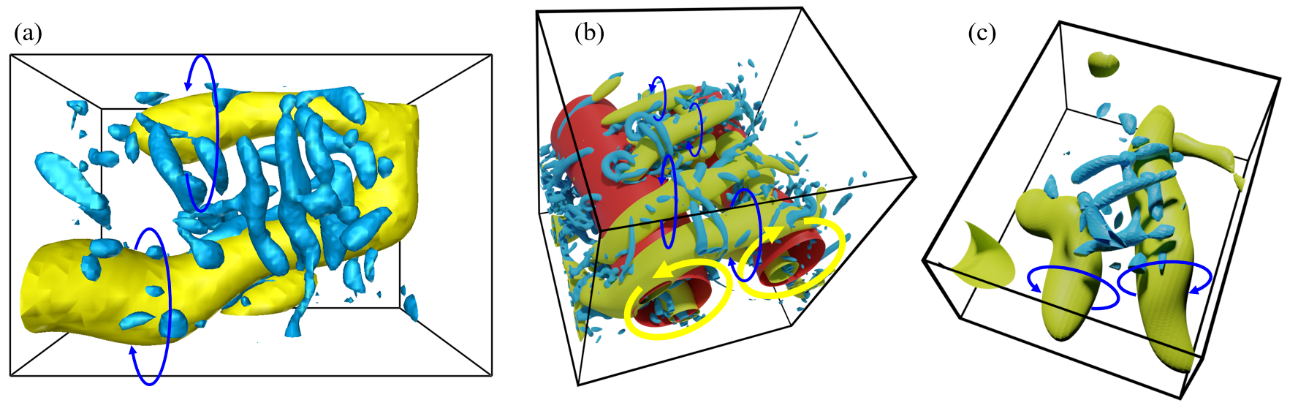
図３：(a) 周期箱乱流，(b) 円柱後流，(c) 平行平板間乱流中の秩序渦の階層．
逆旋回渦対の周囲の引き伸ばし場でより小さな渦が生成されている様子が観察できる．

　図3(a, b)は，壁から離れた領域における渦の階層の生成機構を示す．一方で，壁面があるとその維持機構は一段難しくなる．私たちの今のところの理解は，以下の通りである．まず，壁からの距離に応じて維持機構を考える必要がる．つまり，壁からの距離がHの位置における最大渦の大きさはH程度であると考えられる．これらの渦は，平均流による伸長，あるいは，このスケールにおける自己維持機構（文献(1)の5.7節を参照）より維持される．このとき現れる大規模渦は（巨大な）縦渦である．縦渦は互いに逆旋回するものが，低速・高速ストリークを挟んで互い違いに並ぶ．これらの渦の周囲の伸長場でより小さなスケールの渦が生成され，次第に図3(c)に示すような階層構造が生成される．ただし，このような渦の階層はいわゆる対数層よりも壁から離れた領域でのみ存在する．なぜならば，壁近傍のバッファ層には単一のスケールの渦しか存在しないためである．このため壁乱流において渦の階層を捉えるには十分な対数層が存在する必要がある．実際，摩擦長で定義したレイノルズ数がおよそ4000である平行平板間乱流（図1(c, f)）であっても，テーラー長レイノルズ数は100程度であり，階層が見られるぎりぎりの発達度となる（図2に示すエネルギースペクトルでも，かろうじて-5/3乗則が見られる）．これが図3(c)における階層間の関係が，図3(a, b)ほど明確でない理由である．

　なお，私たちは，乱流境界層についても同様の解析を行った（7, 8）．十分に大きいテーラー長レイノルズ数の乱流境界層の数値シミュレーションはまだまだ難しいが，それでもスケール分解を用いることによって，明確な大規模ヘアピン構造を捉えることができた．詳細は動画(9)をご覧いただきたい．

４. まとめと展望

　乱流は秩序渦の階層からなる．大規模な数値シミュレーションによりその詳細な情報が得られるようになったが，秩序渦の階層を捉えるには工夫が必要である．つまり，エネルギースペクトル（図2）が冪則に従う波数域が見られるような発達した乱流であっても，速度勾配テンソルに基づく素朴な可視化では，ワーム（芋虫）などと呼ばれる微細渦の森（図1(a, b, c)）しか見られない．一方で，スケール分解を施しさえすれば，森の中に秩序が埋まっていることが分かる（図1(d, e, f)）．壁から離れた領域では渦の階層は渦伸長により生成され，これがエネルギーカスケードの主機構であると考えられる．もちろん，このような単純な物理描像に対する批判もある（10）．壁乱流中では，このような明確な描像を数値シミュレーションで捉えるには，まだレイノルズ数が足りない．ただし，図2に示すエネルギースペクトルに明確な冪則が現れるような数値シミュレーションが可能となるのも時間の問題だろう．そうなれば，前節で述べた維持機構が正しいかも明らかになるはずである．楽しみである．

　また，渦の階層が明らかになったことで，乱流輸送現象の理解も急速に進んでいる．とくに，固体粒子と乱流の相互作用（11, 12）については，乱流を渦の集合と考えることで，現象をよく説明できる．上述のように単相乱流の理解が進んだので，今後は混相乱流の理解が加速されるはずである．

謝辞

　紹介した研究の一部は，科学研究費補助金（16H04268，20H02068，20H01819，20J10399，21K20403，23K13253），自然科学研究機構一般共同研究（08KTBL006，11KNSS023，13KNSS043，15KNSS066，17KNSS101，18KNSS108，20KNSS145，22KISS010），HPCI（hp170361，hp180257，hp210207，hp210075，hp220232）の援助を受けて実施しました．

参考文献

(1) 日野幹雄，乱流の科学 – 構造と制御，朝倉出版，2020.
(2) Goto, S., A physical mechanism of the energy cascade in homogeneous isotropic turbulence, J. Fluid Mech. Vol. 605 (2008) 355-366.
(3) Goto, S., Saito, Y. & Kawahara, G., Hierarchy of antiparallel vortex tubes in spatially periodic turbulence at high Reynolds numbers, Phys. Rev. Fluids Vol. 2 (2017) 064603.
(4) Fujino, J., Motoori, Y. & Goto, S., Hierarchy of coherent vortices in turbulence behind a cylinder, J. Fluid Mech. (in press).
(5) Motoori, Y. & Goto, S., Hierarchy of coherent structures and real-space energy transfer in turbulent channel flow, J. Fluid Mech. Vol. 911 (2021) A27.
(6) Goto, S. & Motoori, Y., Hierarchy of coherent vortices in developed turbulence, Rev. Modern Plasma Phys. (submitted).
(7) Motoori, Y. & Goto, S., Scale-dependent enstrophy production rates in a turbulent boundary layer, J. Fluid Sci. Tech. Vol. 14 (2019) JFST0016.
(8) Motoori, Y. & Goto, S., Generation mechanism of a hierarchy of vortices in a turbulent boundary layer, J. Fluid Mech. Vol. 865 (2019) 1085-1109.
(9) https://www.youtube.com/watch?v=mws5a4WkFzI
(10) McKeown, R., Pumir, A., Rubinstein, S. M., Brenner, M. P. & Ostilla-Mónico, R. Energy transfer and vortex structures: Visualizing the incompressible turbulent energy cascade, arXiv:2204.09023v2.
(11) Motoori, Y., Wong, C. & Goto, S., Role of the hierarchy of coherent structures in the transport of heavy small particles in turbulent channel flow, J. Fluid Mech. Vol. 942 (2022) A3.
(12) Oka, S. & Goto, S., Attenuation of turbulence in a periodic cube by finite-size spherical solid particles, J. Fluid Mech. Vol. 949 (2022) A45.
リンク一覧へ戻る
更新日：2023.10.13

↑