流れ　2023年10月号　目次

―　特集テーマ：ASME-JSME-KSME流体工学国際会議　― 巻頭言 （朴，松田，洪） 横風に対する鉄道車両の耐力評価方法と安全な鉄道運行のためのその応用 三須 弥生（JR東日本） 乱流の中の秩序 後藤 晋（大阪大学），本告 遊太郎（大阪大学） LES/粒子シミュレーションによる化学反応を伴う乱流平面噴流の数値解析 シン ジャボオ（名古屋大学）,　渡邉 智昭（名古屋大学大学院）,　長田 孝二（京都大学大学院） 液体ロケットインデューサにおけるキャビテーション不安定現象発生時の翼端漏れ渦キャビテーションの非定常特性 田村 浩紀（東北大学），奈倉 悠人（東北大学），川崎 聡（宇宙航空研究開発機構），伊賀 由佳（東北大学） Water Condensation in PEMFCs at Nano-scale: Insights through Lattice DFT simulations Clint John Cortes OTIC（東京大学），Masazumi ARAO（FC-Cubic），Masashi MATSUMOTO（FC-Cubic），Hideto IMAI（FC-Cubic），Ikuya KINEFUCHI（東京大学） Reconstruction of Fluid Stress Field from Flow Birefringence using Physics-Informed Convolutional Encoder-Decoder (PICED) Daichi IGARASHI（東京農工大学），Shun MIYATAKE（東京農工大学），Jingzu YEE（東京農工大学），Yoshiyuki TAGAWA（東京農工大学） Determination of Permeability in the Volume Penalisation Method with a Smooth Mask Function 辻元 大智（大阪大学），中尾 祐太（大阪大学），辻 拓也（大阪大学），田中 敏嗣（大阪大学），鷲野 公彰（大阪大学） 　｜　リンク一覧にもどる　｜

 

Determination of Permeability in the Volume Penalisation Method with a Smooth Mask Function

辻元 大智， 中尾 祐太， 辻 拓也， 田中 敏嗣， 鷲野 公彰 大阪大学

　2023年7月に開催されたASME-JSME-KSME Fluids Engineering Division (AJK FED) 2023において，光栄にも優秀講演表彰を頂きました．この場をお借りし，選考委員会ならびに日本機械学会流体工学部門の皆様に御礼を申し上げます．本稿では，講演発表内容である，平滑化マスク関数を用いたVolume Penalisation法における浸透率決定方法について紹介させていただきます．

１．緒言

　粒子－流体二相流は多くの工業的用途で扱われ工学上重要であるが，固体－流体間で起こる相互作用は非常に複雑であるために実験による計測は容易ではない．Particle Resolved Direct Numerical Simulation (PR-DNS)は個々の粒子周りの詳細な流れ場を解析することができるため，このような複雑な流れを理解するために有効な手段であると言える．PR-DNSでは，埋め込み境界法の一種であるVolume Penalisation (VP)法⁽¹⁾がしばしば用いられることがある．この手法では，固体粒子を浸透性を持つ多孔質体と見なし，固体表面に直接すべりなし条件を課す代わりに支配方程式に相互作用力項を付与することで固体を表現する．この場合，流体領域および固体領域はマスク関数によって区別され，固体－流体界面を有限の幅で表現した平滑化マスク関数（図1）を用いることで数値振動を抑制できることが報告されている⁽²⁾．Hesterら⁽³⁾とNguyenら⁽⁴⁾は，平滑化マスク関数に対して適切な浸透率を与えるPassive浸透率モデルを提案した．しかし，Hesterらのモデルは浸透率の値が流れ場によらず一定であるため，大きな圧力勾配や外力が働く場合に適用することが難しい．本研究では，圧力勾配や外力の影響を考慮したActive浸透率モデルを開発し，その妥当性を検証する．

２．Volume Penalisation (VP)法

　VP法では，固体－流体間の相互作用力項は以下のように与えられる．

(1)

ここではマスク関数，は浸透率，，はそれぞれ固体と流体の速度，は流体密度である．また，本研究では図1に示すように，流体－固体界面においてに変化する平滑化マスク関数を用いる．この平滑化マスク関数を用いた場合，HesterらとNguyenらは浸透率を決定するモデルを以下のように提案した．

(2)

ここでは固体－流体界面厚さ，は流体動粘度である．このモデルは，レイノルズ数が0に漸近し，流体に圧力勾配や外力が加わらない場合であれば，粒子表面にすべりなし条件を課すのと等価な速度分布を与えることが理論的に示されている．浸透率が流れ場の関数でないことから，本研究ではこれをPassive浸透率モデルと呼ぶ．

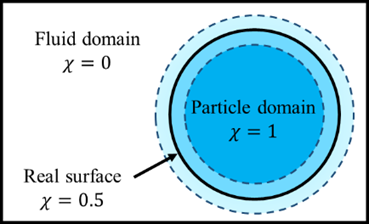
Figure 1. Smooth mask function.

３．Active浸透率モデル

　本研究では，大きな圧力勾配や外力が働く場合に計算精度を向上させるため，Active浸透率モデルを提案する．新たなモデルとして以下の式を仮定する．

(3)

ここでは流れ場に依存した（Activeな）浸透率係数であり，以下のように決定する．まず，固体－流体界面厚さは固体粒子の代表長さに比べて十分小さいと仮定する．この場合，界面内での圧力勾配と外力は固体表面の法線方向に一定と見なすことができる．これらの仮定により，支配方程式は以下のように簡略化できる．

(4)

ここでは流体粘度，は圧力勾配と外力による力の和，添え字は方向の成分を示す．の場合，このモデルはPassive浸透率モデルに漸近し，となる．一方，の場合，最終的に浸透率係数はとなる．実際のは有限であるため，本研究では上記の2つのケースを組み合わせた以下の形をActive浸透率モデルとして提案する．

(5)

４．Active浸透率モデルの妥当性検証

　Active浸透率モデルの妥当性を検証するためにいくつかのシミュレーションを行った．1つ目は，図2に示すような球体が静止壁面に向かって一定速度で移動する系である．この場合は，潤滑効果により粒子－壁面間の圧力が高くなることが知られている．ここでのレイノルズ数は，粒子－壁面間距離はであり，界面厚さは～まで変化させてシミュレーションを行った．

　図3は，流体力におけるシミュレーション結果と解析解（Brennerら⁽⁵⁾）との誤差を示している．この結果から，Active浸透率モデルは界面厚さが大きい場合にPassive浸透率モデルよりもモデル誤差が小さいことが分かる．これはActive浸透率モデルがより正確に相互作用力を捉えられているためである．加えて，図4に示すように，それぞれのモデルによる粒子－壁面間の圧力場を比較すると，Active浸透率モデルでは潤滑による圧力上昇を良好に捉えられていることが分かる．

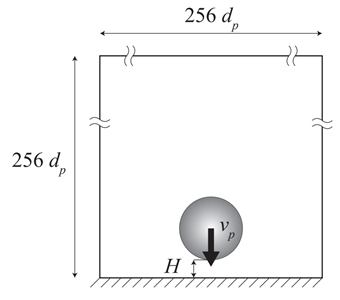
Figure 2. Schematic of a sphere moving towards a wall.

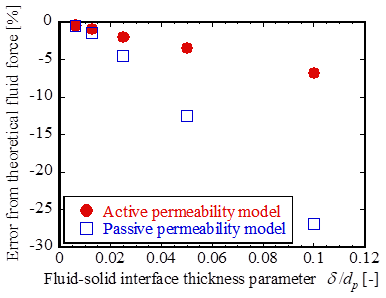
Figure 3. Error of fluid force acting on a particle.

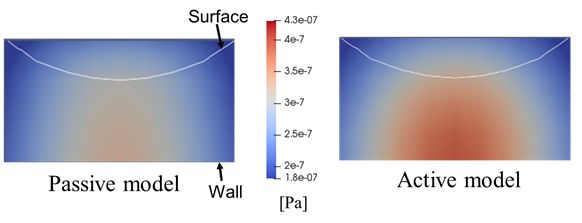
Figure 4. Pressure field at particle-wall gap obtained from each model.

　2つ目は，懸濁液のせん断流れである．図5のように，上下の壁面は一定の速度で移動しており，滑りなし境界条件が適用されている．その他の方向は周期境界を課している．懸濁液の相対粘度は，実効粘度と懸濁媒体粘度の比として定義され，粒子濃度が高くなるにつれて増加することが知られている．希薄な懸濁液ではEinsteinの式⁽⁶⁾で与えられるように線形に増加するが，濃度が上がると粒子間の相互作用により非線形的な増加がみられる．

　図6は，Einsteinの式，MoriとOtotakeの式⁽⁷⁾，Yoshidaらによる実験⁽⁸⁾およびシミュレーションから得られた相対粘度を示している．Einsteinの式との差は粒子間の相互作用の大きさを示す指標であり，粒子濃度が上がるにつれて急激に増加している．2つのモデルの結果は濃度が低い場合には同等であるが，濃度が高い場合には大きな差が見られる．特に，濃度が0.4の場合，Active浸透率モデルにより得られる相対粘度が経験式とよく一致しているのに対し，Passive浸透率モデルは大きく過小評価している．これは，濃度が高いために粒子間の間隙が小さく，大きな圧力勾配が生じるためであると考えられる．

Figure 5. Schematic of suspension under simple shear.

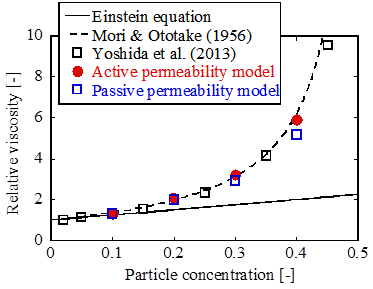
Figure 6. Relative viscosity of suspension.

５．Active浸透率モデルの適用例

　前節の検証結果を踏まえ， Active浸透率モデルを図7(a)のような非球形粒子充填層を通過するクリープ流れに適用した．ここでは，図7(b)に示す楕円体と直方体を用いてそれぞれのシミュレーションを行った．これらの粒子形状の表現には以下に示されるsuperquadric関数⁽⁹⁾を用いた．

(6)

加えて，非球形粒子の平均配向を定量化するために以下のようなHermans配向係数⁽¹⁰⁾を導入した．

(7)

Hermans配向係数は～まで変化し，では粒子は流れ方向に対して垂直であり，では流れ方向に対して平行となる．

　図8は，楕円体と直方体のそれぞれにかかる流体力を比較したものである．この結果から，粒子濃度が0.3の場合には，2つの結果はほとんど同じであるが，濃度が0.4の場合には直方体の方が流体力が大きくなっていることが分かる．これは，濃度が高くなると粒子間の間隙が小さくなり，形状の影響がより顕著になるためであると考えられる．

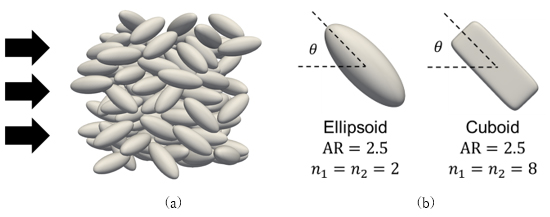
Figure 7. (a) Flow through packed non-spherical particles and (b) non-spherical particles represented by superquadric function.

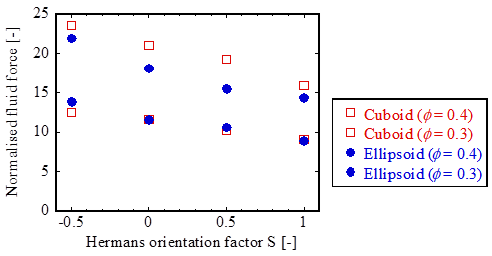
Figure 8. fluid force acting on the ellipsoid and cuboid particles.

６．結言

　本研究では，平滑化マスク関数を用いたVolume Penalisation (VP)法の精度を向上させるために，Active浸透率モデルを提案した．Active浸透率モデルは界面での支配方程式を簡略化したものに基づいて導出され，その浸透率は一定ではなく圧力勾配と外力，流体速度により決定される．このモデルを検証するために，大きな圧力勾配が生じる系を用いてシミュレーションを行った．その結果，提案したモデルは大きな圧力勾配が生じる場合に従来のモデルよりも精度が向上することが確認された．また，Active浸透率モデルを用いて非球形粒子充填層を通過する流れのシミュレーションを行い，粒子濃度が高いほど流体力に与える形状の影響が大きくなることが確認された．

謝辞

　本研究の一部は，九州大学情報基盤研究開発センターの計算資源の提供を受け，数値シミュレーションを行いました．

文献

(1)	P. Angot, C.-H. Bruneau, P. Fabrie, “A penalization method to take into account obstacles in incompressible viscous flows”, Numerische Mathematik, vol. 81, (1999), pp. 497-520.
(2)	D. Kolomenskiy, K. Schneider, “A fourier spectral method for the navier-stokes equations with volume penalization for moving solid obstacles”, Journal of Computational Physics, vol. 228, (2009), pp. 5687-5709.
(3)	E. W. Hester, G. M. Vasil, K. J. Burns, “Improving accuracy of volume penalised fluid-solid interactions”, Journal of Computational Physics, vol. 430, (2021), 110043.
(4)	G. T. Nguyen, E. L. Chan, T. Tsuji, T. Tanaka, K. Washino, “Resolved CFD-DEM coupling simulation using Volume Penalisation method”, Advanced Powder Technology, vol. 32, (2021), pp. 225-236.
(5)	H. Brenner, “The Stokes resistance of an arbitrary particle-IV Arbitrary fields of flow”, vol. 19, (1964), pp. 703-727.
(6)	A. Einstein, “Eine neue bestimmung der moleküldimensionen”, Annalen der Physik, vol. 324, (1906), pp. 289-306.
(7)	Y. Mori, N. Ototake, “On the viscosity of suspensions”, Kagaku Kogaku Ronbunshu, vol. 20, (1956), pp. 488-494.
(8)	Y. Yoshida, T.Katsumoto, S. Taniguchi, A. Shimosaka, Y. Shirakawa, J. Hidaka, “Prediction of viscosity of slurry suspended fine particles using coupled DEM-DNS simulation, Chemical Engineering Transactions, vol. 32, (2013), pp. 2089-2094.
(9)	Barr, “Superquadrics and angle-preserving transformations”, IEEE Computer Graphics and Applications, vol. 1, (1981), pp. 11-23.
(10)	J. J. Hermans, P. H. Hermans, D. Vermaas, A. Weindinger, “Quantitative evaluation of orientation in cellulose fibers from the X-ray fiber diagram”, Recueil des Travaux Chimiques des Pays-Bas, vol. 65, (1946), pp. 427-447.