流れ　2023年10月号　目次

―　特集テーマ：ASME-JSME-KSME流体工学国際会議　― 巻頭言 （朴，松田，洪） 横風に対する鉄道車両の耐力評価方法と安全な鉄道運行のためのその応用 三須 弥生（JR東日本） 乱流の中の秩序 後藤 晋（大阪大学），本告 遊太郎（大阪大学） LES/粒子シミュレーションによる化学反応を伴う乱流平面噴流の数値解析 シン ジャボオ（名古屋大学）,　渡邉 智昭（名古屋大学大学院）,　長田 孝二（京都大学大学院） 液体ロケットインデューサにおけるキャビテーション不安定現象発生時の翼端漏れ渦キャビテーションの非定常特性 田村 浩紀（東北大学），奈倉 悠人（東北大学），川崎 聡（宇宙航空研究開発機構），伊賀 由佳（東北大学） Water Condensation in PEMFCs at Nano-scale: Insights through Lattice DFT simulations Clint John Cortes OTIC（東京大学），Masazumi ARAO（FC-Cubic），Masashi MATSUMOTO（FC-Cubic），Hideto IMAI（FC-Cubic），Ikuya KINEFUCHI（東京大学） Reconstruction of Fluid Stress Field from Flow Birefringence using Physics-Informed Convolutional Encoder-Decoder (PICED) Daichi IGARASHI（東京農工大学），Shun MIYATAKE（東京農工大学），Jingzu YEE（東京農工大学），Yoshiyuki TAGAWA（東京農工大学） Determination of Permeability in the Volume Penalisation Method with a Smooth Mask Function 辻元 大智（大阪大学），中尾 祐太（大阪大学），辻 拓也（大阪大学），田中 敏嗣（大阪大学），鷲野 公彰（大阪大学） 　｜　リンク一覧にもどる　｜

 

LES/粒子シミュレーションによる化学反応を伴う乱流平面噴流の数値解析

シン ジャボオ 名古屋大学,　 渡邉 智昭 名古屋大学大学院,　 長田 孝二 京都大学大学院

１．はじめに

　ASME-JSME-KSME流体工学国際会議2023において，光栄にも日本機械学会若手優秀講演フェロー賞を頂いた．この場を借りて，日本機械学会および選考委員会の皆様に深く御礼申し上げるとともに，講演発表内容を紹介する．

２．緒言

　圧縮性乱流における混合・化学反応過程の解明は，推進システム設計など工学的に重要である．近年，計算機の発達に伴いラージエディシミュレーション（LES）の活用が様々な流体現象に対して進められている．化学反応を伴う乱流にLESを適用する場合，化学物質の輸送方程式に含まれる反応項のサブグリッドスケール（SGS）モデルが必要となる．モデルは反応や流れの種類に依存することが知られており，反応項に対するSGSモデルの直接的な適用を避けることを目的として，流れ場に対するLESを化学物質の混合・反応を取り扱う別の計算手法と組み合わせる試みがなされている⁽¹⁾．本研究では，混合・反応場をラグランジュ的に解析する粒子シミュレーション（Lagrangian Particle Simulation: LPS）とLESを組み合わせた計算手法^(2,3)の有効性について調査した．乱流中の混合・反応を計算粒子によりラグランジュ的に解析する場合，分子拡散項に対するモデルが必要となる。非圧縮性乱流中の物質拡散に対して提案された混合体積モデル^(3,4)を圧縮流れに適用し，モデルの有効性を明らかにした．

３．LES/LPS

　LESとLPSを組み合わせた計算手法により等温二次化学反応A+B→Pを伴う圧縮性乱流平面噴流の数値解析を行った．LESでは圧縮性流れに対するNavier–Stokes式を解く．LPSでは化学物質の質量分率および混合分率（反応により変化しないスカラー量）の輸送方程式を計算粒子により解析する．無次元化されたとの輸送方程式は以下の式により表される．

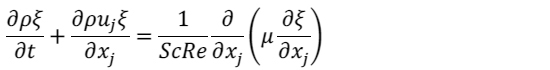	(1)
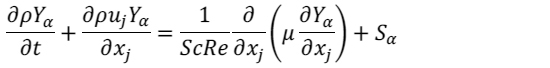	(2)

は密度，は速度ベクトル，は粘性係数，は化学種に対する反応項であり，およびはそれぞれReynolds数とSchmidt数である．本研究で取り扱う支配方程式および化学反応についての詳細は文献5に示されている通りである．LPSにおいて，各計算粒子には位置およびスカラーの情報が与えられる．番目の計算粒子の位置を，粒子位置における質量分率および混合分率をと表記する．LES/LPSにおいて計算粒子の時間発展は，以下の式により表される．

	(3)
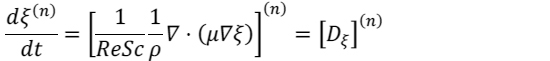	(4)
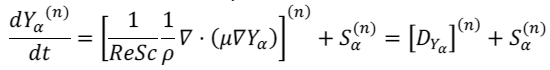	(5)

LESにより得られる粗視化された速度を粒子位置に補間することで粒子位置の時間変化を計算する．およびは分子拡散項であり，混合モデルにより計算される．反応項については粒子位置で定義されるにより直接計算できる．流れ場に対するLESを式(3, 4, 5)に基づくLPSと併せて実行することで，乱流中の化学反応場の数値解析が可能となる．

　LPSでは分子拡散項の正確なモデル化が重要となる．分子拡散に対するモデルとして著者らにより考案された混合体積モデルを圧縮性流れに拡張し，その有効性を調査した．混合体積モデルでは，注目する粒子の質量分率や混合分率をその近傍の複数の粒子（混合粒子）により定義される局所平均値へと緩和させる過程により分子拡散項をモデル化する．モデルの詳細は文献3, 4に示されている他，本モデルの圧縮性流れへの拡張が文献6で議論されている．混合体積モデルのパラメータである混合率の算出には，スカラー散逸率の混合粒子平均値のモデル化が必要である．スカラー散逸率に対するSGSモデル⁽⁷⁾を，混合粒子平均値に対するモデルへと拡張⁽⁸⁾し混合率の計算に用いた．

４．化学反応を伴う圧縮性乱流平面噴流の数値シミュレーション

　等温二次化学反応A + B→Pを伴う圧縮性乱流平面噴流に対するLES/LPSを実施した．ここでは時間発展型平面噴流を計算対象とした（図1）．時間発展型平面噴流は流れ(x)方向およびスパン(z)方向に周期境界を課した計算領域において時間とともに方向に発達する．初期条件として，を中心とする幅の領域に初期噴流速度を，噴流外部において静止流体を仮定する．噴流と外部流体はそれぞれ反応物質AとBを含む．各物質の質量分率を，，とすると，混合分率はにより定義される．は化学反応による影響を受けないスカラー量であり，初期条件では，噴流外部において，噴流内部においてとなる．LPSにおいておよびの発達を解析し，質量保存則を用いることでからを算出した．噴流マッハ数および2.6の条件について計算を実施した．噴流レイノルズ数は，ダムケラー数は，シュミット数はである．

　計算領域を× ×とした．LES/LPSには文献9, 10の計算コードを用いた．LESではローパスフィルタに基づく陰的SGSモデルを用いた．各方向の計算格子数をとし，および方向に等間隔格子を，方向に噴流近傍で格子幅が小さくなる不等間隔格子を用いた．LPSにおいて480,000個の計算粒子を用いた．初期条件として粒子をの領域にランダムに配置した．乱流のDNSデータベースに基づく混合体積モデルの検証結果に基づき，混合粒子数を12とした^(4,8)．また，同流れ場のDNSも合わせて実施し，LES/LPSの検証に用いた．DNSには文献11のコードを使用した．

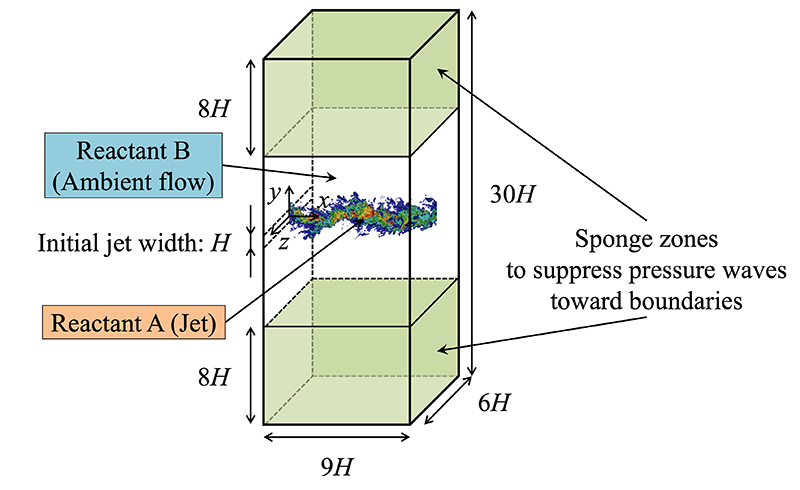
図1　化学反応を伴う時間発展型平面噴流

５．計算結果

　における生成物Pの質量分率の平面における分布を図2に示す．噴流初期速度・幅により無次元化された時刻における分布が可視化されている．この時刻において噴流は十分に発達している．噴流中心から離れた領域において質量分率が大きい値をとる傾向が見られる．LES/LPSにより得られたの分布は，その広がりや噴流内部の分布についてDNSと同様の傾向を示している．図3にの時間変化の動画を示す．噴流と外部流体の境界領域における活発な反応によりが増加し，噴流中心付近へ輸送されることでは噴流内部に広く分布する．同様の結果がDNSにおいても得られている．

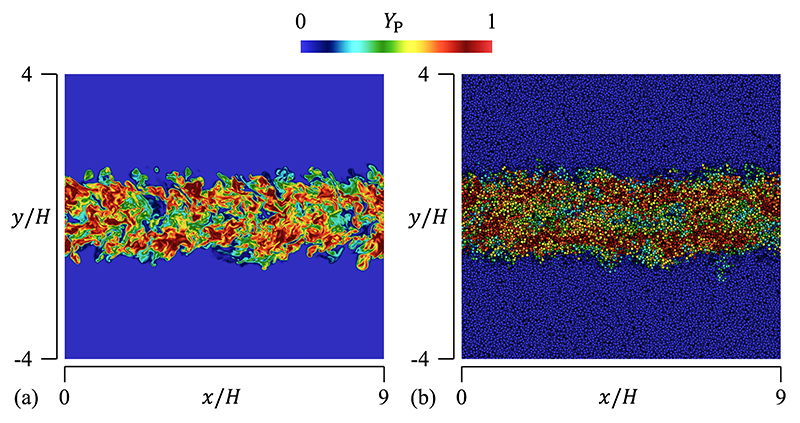
図2　生成物Pの質量分率の平面における分布（，）：（a）DNS，（b）LES/LPS

図3　生成物Pの質量分率の時間発展（）

　図4に各マッハ数において得られた反応物A，Bの平均質量分率の方向分布を示す．いずれも噴流が十分に発達したにおいて得られたものであり，DNSとLES/LPSの結果が比較されている．位置は平均混合分率の半値幅により無次元化されている．高マッハ数条件では噴流の発達が遅れるため，混合・反応の進行も抑制される．そのため，では反応物Aが反応によりほぼ全て消費され噴流内部でもとなる一方，では噴流中心付近でが大きい値をとる．高マッハ数条件では噴流内のAが残存しており，外部から取り込まれたBのほとんどが反応により消費されるため，では噴流中心付近のが小さくなる．こうした平均質量分率のマッハ数依存性がLES/LPSによりよく再現されていることが確認できる．

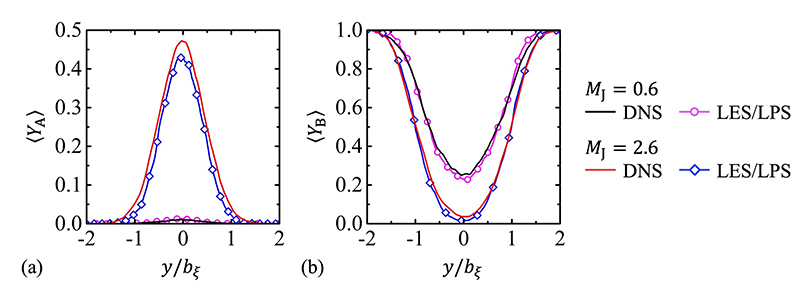
図4　平均質量分率の方向分布（） (a) 反応物A，(b) 反応物B

６．結言

　圧縮性流れに拡張された混合体積モデルを用いたLES/LPSにより圧縮性乱流噴流中の化学反応の数値解析を行った．DNSデータとの比較により，本手法が高マッハ数流れにおける化学反応場を精度よく予測できることを確認した．従来の混合モデルと異なり，混合体積モデルにおける計算パラメータは乱流の小スケール統計量の普遍的特性を基に決定されるため，流れ場に応じたパラメータの調整が不要である⁽⁸⁾．また，高シュミット数に特徴づけられる液中の反応場への応用も進められている⁽¹²⁾．本手法が様々な乱流中の化学反応場の数値予測に利用されることが期待される．

７．謝辞

　直接数値計算には名古屋大学のスーパーコンピュータ「不老」を用いた（名古屋大学HPC計算科学連携研究プロジェクト）．また，本研究の一部はJSPS科研費（JP22K03903）の助成の基で実施された．ここに記して謝意を表する．

８．文献

(1)	D. C. Haworth, Progress in probability density function methods for turbulent reacting flows, Prog. Energy Combust. Sci., Vol.36, (2010), pp. 168–259.
(2)	C. Le Ribault, and S. Simoens, and I. Vinkovic, Hybrid large eddy simulation/Lagrangian stochastic model for turbulent passive and reactive scalar dispersion in a plane jet, Chem. Eng. Commun., Vol. 199, (2012), pp. 435–460.
(3)	T. Watanabe, Y. Sakai, K. Nagata, Y. Ito, and T. Hayase, LES–Lagrangian particle method for turbulent reactive flows based on the approximate deconvolution model and mixing model, J. Comput. Phys., Vol. 294, (2015), pp. 127–148.
(4)	T. Watanabe and K. Nagata, Mixing model with multi-particle interactions for Lagrangian simulations of turbulent mixing, Phys. Fluids, Vol. 28, (2016), 085103.
(5)	Z. Pouransari, G. Brethouwer, and A. V. Johansson, Direct numerical simulation of an isothermal reacting turbulent wall-jet, Phys. Fluids, Vol. 23, (2011), 085104.
(6)	Y. Tai, T. Watanabe, and K. Nagata, Modeling of molecular diffusion and thermal conduction with multi-particle interaction in compressible turbulence, Phys. Fluids, Vol. 30, (2018), 035108.
(7)	A. W. Cook and W. K. Bushe, A subgrid-scale model for the scalar dissipation rate in nonpremixed combustion, Phys. Fluids, Vol. 11, (1999), pp. 746–748.
(8)	S. Tanaka, T. Watanabe, and K. Nagata, Multi-particle model of coarse-grained scalar dissipation rate with volumetric tensor in turbulence, J. Comput. Phys., Vol. 389, (2019), pp. 128–146.
(9)	Y. Tai, T. Watanabe, and K. Nagata, Implicit large eddy simulation of passive scalar transfer in compressible planar jet, Int. J. Numer. Methods Fluids, Vol. 93, (2021), 1183–1198.
(10)	Y. Tai, T. Watanabe, and K. Nagata, Multi-particle models of molecular diffusion for Lagrangian simulation coupled with LES for passive scalar mixing in compressible turbulence, Compt. Fluids, Vol. 221, (2021), 104886.
(11)	R. Nagata, T. Watanabe, and K. Nagata, Turbulent/non-turbulent interfaces in temporally-evolving compressible planar jets, Phys. Fluids, Vol. 30, (2018), 105109.
(12)	T. Watanabe and K. Nagata, LES-Lagrangian-particles-simulation of turbulent reactive flows at high Sc number using approximate deconvolution model, AIChE J., Vol. 62, (2016), pp. 2912–2922.