流れ　2023年10月号　目次

―　特集テーマ：ASME-JSME-KSME流体工学国際会議　― 巻頭言 （朴，松田，洪） 横風に対する鉄道車両の耐力評価方法と安全な鉄道運行のためのその応用 三須 弥生（JR東日本） 乱流の中の秩序 後藤 晋（大阪大学），本告 遊太郎（大阪大学） LES/粒子シミュレーションによる化学反応を伴う乱流平面噴流の数値解析 シン ジャボオ（名古屋大学）,　渡邉 智昭（名古屋大学大学院）,　長田 孝二（京都大学大学院） 液体ロケットインデューサにおけるキャビテーション不安定現象発生時の翼端漏れ渦キャビテーションの非定常特性 田村 浩紀（東北大学），奈倉 悠人（東北大学），川崎 聡（宇宙航空研究開発機構），伊賀 由佳（東北大学） Water Condensation in PEMFCs at Nano-scale: Insights through Lattice DFT simulations Clint John Cortes OTIC（東京大学），Masazumi ARAO（FC-Cubic），Masashi MATSUMOTO（FC-Cubic），Hideto IMAI（FC-Cubic），Ikuya KINEFUCHI（東京大学） Reconstruction of Fluid Stress Field from Flow Birefringence using Physics-Informed Convolutional Encoder-Decoder (PICED) Daichi IGARASHI（東京農工大学），Shun MIYATAKE（東京農工大学），Jingzu YEE（東京農工大学），Yoshiyuki TAGAWA（東京農工大学） Determination of Permeability in the Volume Penalisation Method with a Smooth Mask Function 辻元 大智（大阪大学），中尾 祐太（大阪大学），辻 拓也（大阪大学），田中 敏嗣（大阪大学），鷲野 公彰（大阪大学） 　｜　リンク一覧にもどる　｜

 

Reconstruction of Fluid Stress Field from Flow Birefringence using Physics-Informed Convolutional Encoder-Decoder (PICED)

Daichi IGARASHI Shun MIYATAKE Jingzu YEE Yoshiyuki TAGAWA 東京農工大学

1.　緒言

　AJK FED 2023において，栄えある優秀講演表彰を頂いた．この場を借りて，本学会関係者及び選考委員会の皆様に御礼申し上げるとともに，講演内容を以下に紹介する．

　流体中の応力場を求めるには，流速分布から構成方程式を用いて算出する必要がある．そのため，構成方程式が不明な複雑流体を対象とする場合，流速分布から応力場を算出することが困難となる．例えば，複雑流体の一つに血液がある．先行研究では数値計算により血液が血管に与える応力を取得することを試みたものもあるが⁽¹⁾，上述の通り数理モデルの学術的問題から信頼に欠ける．そのため，血管上にこぶができる脳動脈瘤の発生原因は未だ解明されていない．

　武藤ら⁽²⁾は，高速度偏光カメラを用いて非定常流体の光学的位相差∆ [m]とその配向方向(方位)φ [rad]の可視化に成功した．位相差とは，応力によるひずみに起因して発生する光波のずれを表し，方位とはその主応力の方向を表す．したがってこれらの値は応力σ [Pa]と関係する．そのため，位相差及び方位の可視化は，複雑流体の応力場を非接触で直接測定することを可能とする．しかし，偏光カメラで取得可能な情報は複雑な行列計算による積算値であり，応力場を得るために再構成が必要となる．

　先行研究では，簡易形状において応力場構築に成功しているものの^(3),(4)，複雑形状においては理論解が不明な非線形問題であるため再構成が困難である．そこで本研究では，非線形問題を扱える機械学習に注目した．近年，機械学習を援用した画像再構成は，流体分野のみならず様々な分野で行われている⁽⁵⁾．以上から本研究では，位相差と方位の積算値から流体応力場を導出する機械学習モデルの構築を目的とする．本研究では，物理方程式を考慮可能なモデルであるPhysics-Informed Neural Network⁽⁶⁾に注目した．本手法を用いて，物理現象に即した応力場の予測を試みる．

2.　実験・機械学習手法

　位相差と方位を取得するために行った実験について，装置を図1aに示す．光源から放出する光は，計測対象を通った後に高速度偏光カメラに入射する．計測対象は，Laneら⁽⁷⁾が作成した流路を用いた．これは，図1aに示すように流れ場に対してcosカーブの瘤を設置した流路である．なお，本流路は奥行き方向に十分な長さがあるため，奥行き方向の流れ場を無視することができる．作動流体としては，光弾性流体であるCNC-HS-FD水溶液(0.5 wt%)を流す．光弾性流体とは，応力負荷により位相差を発現する流体である．機械学習には，大量の実験データが必要になる．そこで本研究では，シリンジポンプおよび偏光カメラをPCにより同期し，自動で制御するシステムを構築した．これにより，同じ液体を押し引きすることで半永久的に作動流体を流し続けることができる．この自動化実験装置を用いて，流量Qのみを変化させ，Q = 20-50 mL/minの範囲で1 mL/min刻みでデータを取得した．

　実験により取得した位相差及び方位の分布をそれぞれ図2b(i),(ii)に示す．図2b(i)では，瘤近傍で位相差が大きくなっており，当部で応力の絶対値が大きくなっていることが考察できる．一方で，方位φは壁面に対して45°の値となっている．これは，壁面で流れによる剪断応力が発生していることを示している．学習の簡単化のために，本画像をそれぞれ図に赤破線で囲んだ位置でトリミングした．Q = 35 mL/minをテストデータとして除き，残りのQ = 20-50 mL/minの20データずつ，合計600データを学習データとした．機械学習の正解データとなる応力分布は，COMSOL Multiphysicsを用いて数値シミュレーションにより取得した．実験に用いた流路と同じジオメトリを作成し，CNC-HS-FDの粘度分布と近いCarreau-Yasudaモデルに従う流体を流した．また，今回は二次元流を対象としたため，応力テンソルは次式が成り立つ．

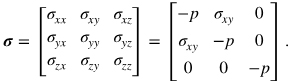(1)

ただし，pは大気圧を表す．上式より，今回データごとに変化する値はσ_xyのみのため，出力する応力としてはこの値のみを用いた．以上から，位相差と方位の分布を入力，応力分布を出力として機械学習を行った．

　機械学習のモデルには，図2に示すPhysics-Informed Convolutional Encoder-Decoder (PICED)を用いた．これは，三次元的な時空間情報から三次元的な時空間情報を生成可能なモデルであり⁽⁸⁾，位相差と方位の画像から応力場の画像を生成可能とする．また，損失関数に物理方程式を入れることで物理現象を考慮した予測ができる．本稿では，物理方程式としてCarraeu-Yasudaモデルにおける粘性則および連続の式を用いた．そこで，物理方程式にx, y軸方向の速度u, vが必要となるため，今回は速度も出力対象とした．平均二乗誤差(MSE)を用いたデータ誤差(data loss)をL_data，物理方程式を用いた残差(residual loss)をL_PDEとし，全体の損失関数L_totalを次式で定義する．

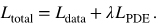(2)

なお，λはフィッティングパラメータを表し，λ=10^-2とした．さらに，L_data, L_PDEはそれぞれ次式(2), (3)で表せる．

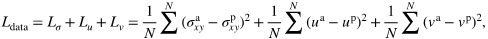	(3)
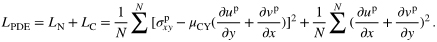	(4)

ただし，Nは一画像のデータ点数，σ_xy, u, vはそれぞれ応力およびx, y軸方向速度を示し，上付き文字a, pはそれぞれ正解値，予測値を示す．また，μ_CYはCarraeu-Yasudaモデルにおける粘性係数を表す．

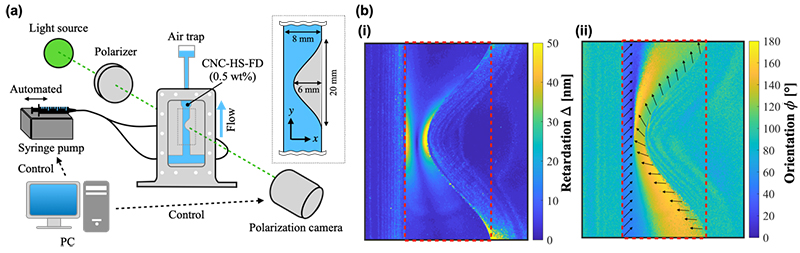
Fig. 1 (a) Schematic of the automated experimental setup (b) Examples of the images of (i) retardation and (ii) orientation captured by the polarization camera.

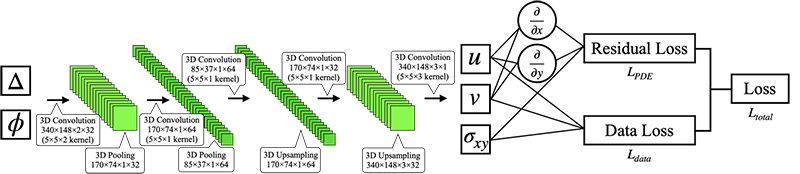
Fig. 2 Architecture of the Physics-Informed Convolutional Encoder-Decoder (PICED).

  3.　結果・考察

　正解データである数値計算結果(CFD)およびPICEDによる応力場σ_xy，速度場u, vの再構成結果を図3に示す．なお，損失関数にMSEのみを用いた場合のCNNによる再構成結果も同図に示す．本結果から，応力に関してCFDに対するPICEDの平均相対誤差MAPEを求めると，1.74 %となり，十分に高い精度を確認した．ただし，一般的な機械学習で用いるCNNの結果もMAPEが2.24 %とPICEDと同様高い精度を確認した．一方で，図3におけるy方向速度vの結果における赤丸で囲った領域に注目すると，CNNの結果では値が急激に小さくなる結果が得られているのに対し，同じ位置のPICEDの結果ではその部分が滑らかに補正されていることがわかる．これは，PICEDでは連続の式を考慮しており，それが値の急激な変化を抑制したと考えられる．

　さらに，CNNとPICEDの物理方程式の影響を調査するために，式(4)中の粘性則および連続の式による残差を表すL_NおよびL_Cの値を調査した．その結果，テストデータにおいてCNNではL_N = 1.20×10^-2, L_C = 6.00，PICEDではL_N = 9.85×10^-3, L_C = 5.13となった．これらの値から，両者に大きな値の差は見られなかった．これは，CNNにより正解画像と非常に近い値の予測に成功したため，物理方程式により得られる数値計算結果に近い値となったためであると考える．一方で，PICEDの方がL_NおよびL_Cの値が小さくなっていることから，物理方程式を満たさない箇所を補正することができたと考えられる．以上から，本手法により物理現象に即した予測が可能な機械学習モデルの構築に成功したと考える．

 
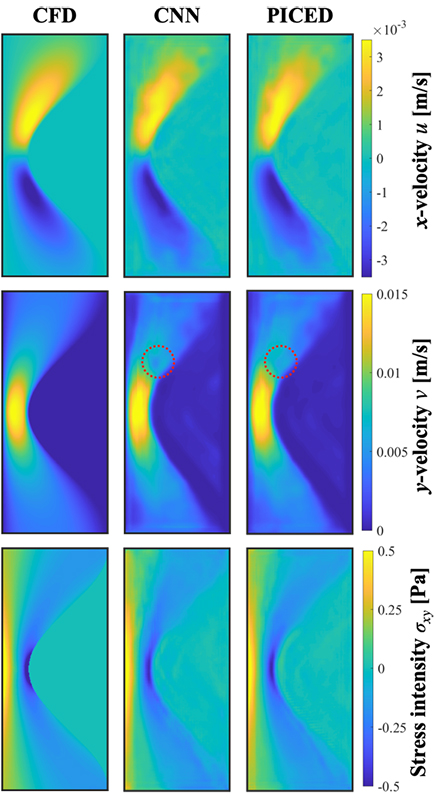
Fig. 3 Velocity u, v and stress intensity σ_xy: calculation results of CFD, prediction results of CNN and PICED.

4.　結言

　本研究では，高速度偏光カメラで得られる位相差と方位の積算値から，流体応力場を取得する機械学習モデルを構築することを目的とした．本稿では，Laneらが作成した二次元流路を対象として，3D Physics-Informed Convolutional Encoder-Decoderにより機械学習を行った．その結果，内挿データの応力分布を1.74 %と高い精度で予測に成功した．また，物理方程式として入れ込んだ粘性則および連続の式を満たすように学習し，通常の機械学習モデルよりも物理現象を考慮可能なモデルの構築に成功した．この知見は，流体応力場を構築する上でより実現象に即した予測をするために非常に重要な知見となる．今後は，より複雑な形状の流路を対象として，多方向から撮影した偏光計測画像から三次元流体応力場の構築を目指す．

　最後に，本講演会において大変貴重なご助言やご質問を下さった先生方，本ニューズレターの執筆の機会を与えて下さった日本機械学会関係者の皆様や選考委員会の皆様に心から感謝の意を表する．

文献

(1)	Shojima, M., et al., “Magnitude and role of wall shear stress on cerebral aneurysm: computational fluid dynamic study of 20 middle cerebral artery aneurysms.”, Stroke, (2004), 35(11), 2500-2505.
(2)	Muto, M., et al., “Non-contact and non-steady rheo-optical measurement of hydrodynamic stress fields inside a cylindrical tube.”, 20th International Symposium on Application of Laser and Imaging Techniques to Fluid Mechanics, (2022).
(3)	Nakamine, K., et al., “Integrated photoelasticity measurements of a three-dimensional laminar flow: second-order stress terms in the stress-optic law.”, Optica Open, (2023).
(4)	Yokoyama, Y., et al., “Integrated photoelasticity in a soft material: phase retardation, azimuthal angle, and stress-optic coefficient.” Optics and Lasers in Engineering, 161, (2023), 107335.
(5)	Mescheder, L., et al., “Occupancy networks: Learning 3d reconstruction in function space.”, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, (2019), pp. 4460-4470.
(6)	Karniadakis, G. E. et al., “Physics-informed machine learning.”, Nature Reviews Physics, 3(6), (2021), 422-440.
(7)	Lane, C., “Shear rate imaging using a polarization camera and birefringent aqueous cellulose nanocrystal suspensions.”, Ph.D. thesis, ETH Zurich, (2022).
(8)	Shan H., et al., “3-D convolutional encoder-decoder network for low-does CT via transfer learning from a 2-D trained network.”, IEEE transactions on medical imaging, Vol. 37, No. 6, (2018), pp. 1522-1534.