流れ　2023年11月号　目次

―　特集テーマ：2023年度年次大会　― 巻頭言 （森，金川） なぜ間違いは伝達・拡散するのか？（流体力学に関する誤認識の拡散とその防止） 石綿 良三（神奈川工科大学） デジタルツイン数値タービンへの道 山本 悟（東北大学） 多チャンネルマイクアレイを用いた乱流境界層と翼・平板結合部における乱流壁面圧力変動場の計測 中 吉嗣（明治大学） 感圧・感温塗料を用いた壁面の圧力・温度場計測とその応用 江上 泰広（愛知工業大学） MEMS差圧センサを用いた流れ計測 高橋 英俊（慶應義塾大学）， 岸本 卓大（慶應義塾大学），小原 慧（慶應義塾大学），嶋田 恭大（慶應義塾大学） フレキシブルシートセンサを用いた流れセンシング 元祐 昌廣（東京理科大学） 　｜　リンク一覧にもどる　｜

 

多チャンネルマイクアレイを用いた乱流境界層と翼・平板結合部における乱流壁面圧力変動場の計測

中 吉嗣 明治大学

1.　緒言

　乱流中の圧力変動は速度変動と共に乱流運動を記述する基本的な物理量である．低速空気流の圧力変動の測定には，感度が高いことと周波数特性が平坦であることからマイクロフォンが圧力センサとして多く用いられる．近年のIoT技術の進歩によってマイクロフォンのデジタル化，小型化，低価格化が進み，多チャンネルマイクアレイを用いた圧力変動場計測が可能となった．著者らは乱流境界層における168chの圧力変動計測⁽¹⁾，翼平板流れにおける768chの圧力変動と速度場の同時計測⁽²⁾などを実施している．本発表ではこれらの計測結果を紹介し，マイクアレイを用いた多チャンネル圧力変動測定技術の可能性について述べる．

2.　乱流圧力変動計測用多チャンネルマイクアレイ

　本研究で開発した多チャンネルマイクアレイはマイクアレイ基板とFPGAコントローラで構成される．マイクアレイ基板にはデジタルMEMSマイクロフォン（INMP621, TDK InvenSense）が搭載されている．マイクロフォンの配置は流れ場の特性に応じて変更することができ，これまでに標準的な1列アレイの他，Fig. 1に示すような乱流境界層においてスパン方向の空間解像度を向上させる目的で作成した2列オフセット配置アレイ⁽¹⁾，瞬時の壁面圧力勾配ベクトルを測定するための2列アレイ⁽³⁾，曲面に適用可能なフレキシブルアレイを製作している．

Fig. 1  A 56ch MEMS microphone array.

　FPGAコントローラはマイクを駆動するための電源と基準クロックを供給し，マイクからの出力信号を受け取ってディスクに記録する．本研究ではFPGA/SoCボード（ZYBO, Digilent）を用いて32ピンをマイクとの信号入出力に用いた．マイクからの出力信号は1bitのPDM (Pulse Density Modulation) 信号で，基準クロックに同期した入力をバイナリデータとしてSSDに記録する．

　SSDに記録されたPDM信号にデシメーションフィルタを施すことで各chの圧力波形を復元する．フィルタ係数は次数64の移動平均フィルタ係数を畳み込み，次数127のsinc2フィルタとしたものを用いて，Matlabのfiltfilt関数を用いてフィルタ処理を行った．

　測定データに含まれる背景雑音ノイズは多チャンネルマイクアレイデータのPOD（Proper Orthogonal Decomposition）モード解析によってノイズを多く含む低次モードを除去した．

3.　乱流境界層における圧力変動場の測定および翼・平板結合部流れにおける圧力変動場と速度場の同時測定

　乱流境界層の壁面に56chの2列オフセット配置アレイを配置し，壁面圧力変動の時空間分布を測定した例をFig. 2に示す．本計測の条件は摩擦レイノルズ数 ，境界層厚さ mmであり，測定孔の直径 とスパン方向の測定孔間隔  は壁単位長さでそれぞれ ， である．これらは壁面近傍の乱流構造を捉えるために十分な空間解像度である．Figure 2には壁面圧力変動の正負の間欠的なパターンが確認できる．Figure 3に壁面圧力変動のRMS値，Fig. 4に壁面圧力変動の確率密度関数を示す．マイクアレイによって得られた壁面圧力変動のRMS値を過去の研究で得られたデータと比較すると，若干変動の大きさを過小評価する傾向にあるものの，おおむね良い一致を示した．過小評価の理由はノイズ処理操作で除去したPODモードに圧力変動信号が含まれていたためであると考えられる．また，Fig. 4に示す通り，本手法によって得られた確率密度関数は正規分布よりも裾野が広い分布をしており，壁面圧力変動の間欠性を表している．これらの瞬時場と統計的評価によってマイクロフォンアレイの乱流壁面圧力変動計測手法としての妥当性が検証されている．

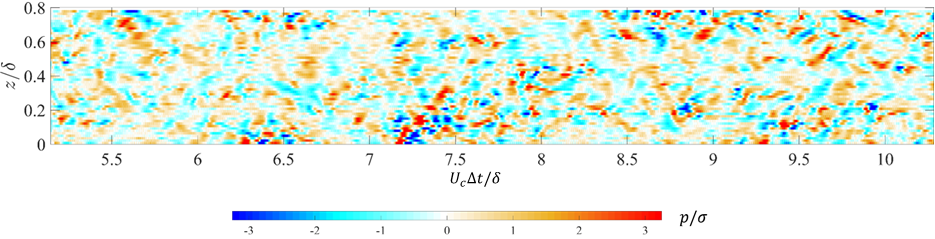
Fig. 2  Instantaneous space-time distribution of the wall pressure fluctuations in a turbulent boundary layer.

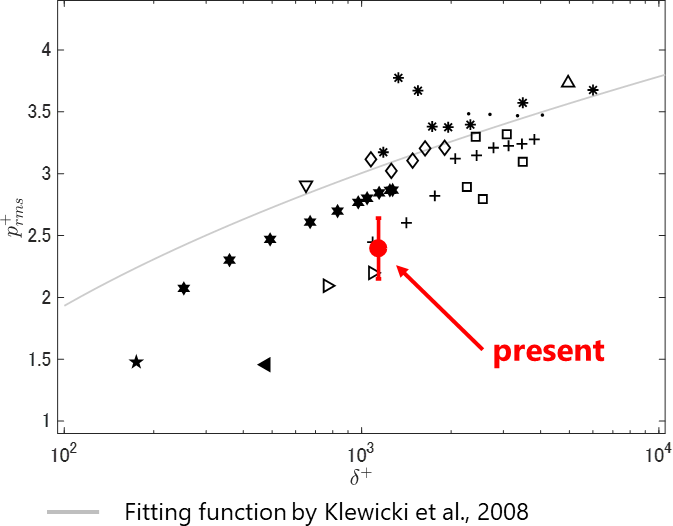
Fig. 3  Comparison of RMS values of the wall pressure fluctuations. Different symbols correspond to different data sources indicated in Klewicki et al., 2008⁽⁴⁾.

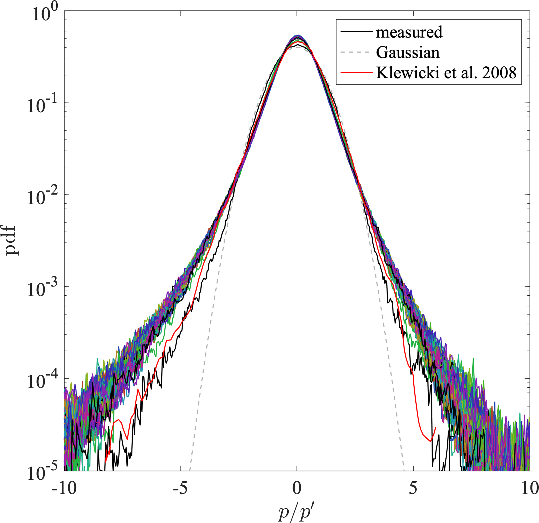
Fig. 4  Probability density functions of the wall pressure fluctuations measured by the microphone array.

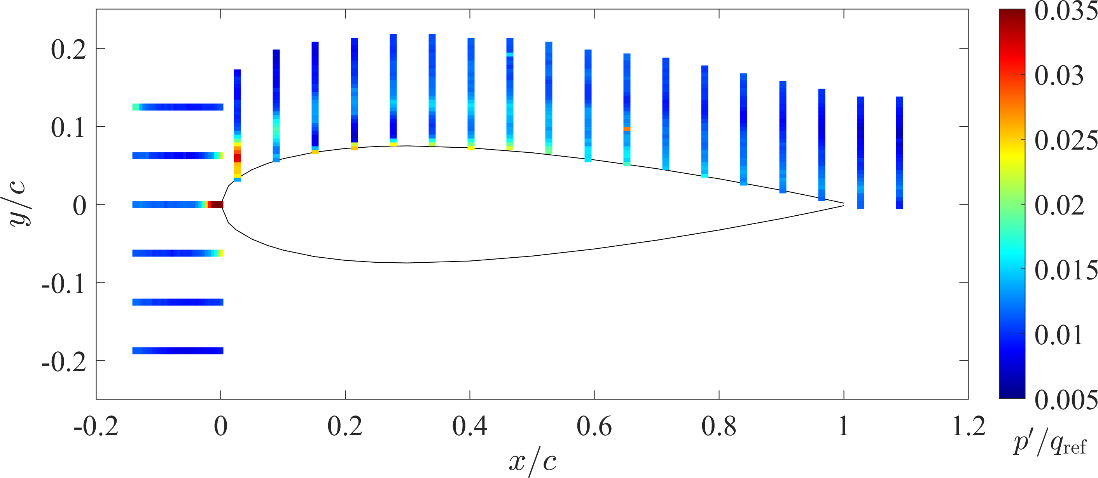
Fig. 5  Distribution of the RMS values of the pressure fluctuations on the flat plate in the wing-flat plate juncture flow. The color is normalized by the dynamic pressure .

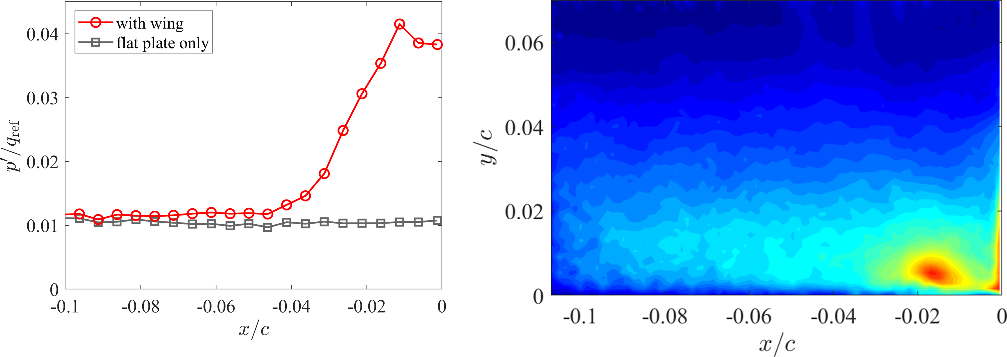
Fig. 6  Distributions of the RMS values of the wall pressure fluctuations on the stagnation line (a), and the wall normal velocity fluctuations in the stagnation plane(b).

　翼・平板結合部には馬蹄形渦やコーナー剥離といった特徴的な3次元流れ構造があり，圧力変動の原因となっている．本研究では平板上の圧力変動場と翼のよどみ面上での粒子画像流速測定法（PIV）による速度場の同時計測を行った．Figure 5には平板上に設置された672chのマイクによって得られた圧力変動強度の空間分布を示す．これは28chの1列マイクアレイ基板を24枚用いた計測である．圧力変動の分布から，よどみ線上に観察される強い圧力変動の下流方向への発達が確認できる．また，Fig. 6に示すよどみ線状の壁面圧力変動と，よどみ面上の平板垂直方向速度変動強度分布には，翼近傍において馬蹄形渦の揺動によると思われる強い変動がみられる．

　速度変動場と壁面圧力変動場の対応を見るために，PODモード解析を行った．壁面圧力変動のPOD空間モードと時間係数，平板垂直方向速度変動のPOD空間モードと時間係数とする．壁面圧力と速度変動の主要なモード（上位20モード）について各モードに対応する  と  の相互相関係数を計算する．相関の高い組み合わせが速度場と圧力場の関係が深いモードとして，そのモード形状と再構築した速度場・壁面圧力場の統計量を評価する．Figure 7に圧力と平板垂直方向速度 の主要モードの相互相関係数を示す．Figure 8に壁面圧力変動と相関の高い速度場の主要モードを示す．これらの結果から，よどみ線上の圧力変動は大きさ0.2c程度の平板垂直方向速度変動構造に関連していることが明らかとなった．

　本マイクロフォンアレイを用いることで，壁面圧力変動から乱流構造に関する情報を得られる．

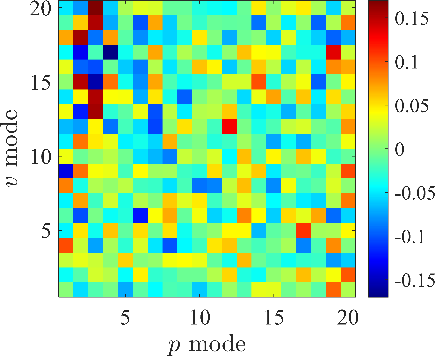
Fig. 7  Correlation coefficients between the POD mode coefficients of principal modes of the wall pressure and wall normal velocity fluctuations.

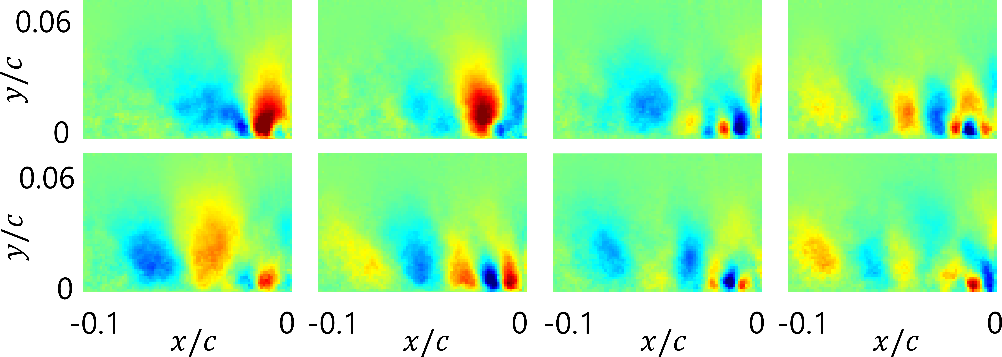
Fig. 8  Shapes of the principal POD modes of the wall normal velocity fluctuations having a significant correlation with the wall normal velocity fluctuations.

4.　結言

　本稿では多チャンネルマイクアレイを用いた乱流壁面圧力変動場の測定手法について解説した．多チャンネルマイクアレイの構成について乱流境界層と翼・平板結合部流れにおける測定結果を示し，本手法の有効性を示した．

文献

(1)	Naka, Y. and Miyajima, M., “A 56ch MEMS microphone array for measuring wall pressure fluctuation field”, TSFP11 (2019).
(2)	中吉嗣, 林大我, “翼・平板結合部流れにおける672ch壁面圧力変動場と翼前縁近傍2D2C速度場の同時計測”, 流体力学会年会2022.
(3)	土屋晶裕，中吉嗣，“2列マイクロフォンアレイを用いた乱流境界層における壁面圧力勾配変動の測定”，日本機械学会第100期流体工学部門講演会 (2022).
(4)	Klewicki, J. C., Priyadarshana, P. J. A., and Metzger, M. M. “Statistical structure of the fluctuating wall pressure and its in-plane gradients at high Reynolds number”, J Fluid Mech, 609 (2008), 195-220.