流れ　2024年11月号　目次

―　特集テーマ：2024年度年次大会　― 巻頭言 （森，金川） レイノルズ応力輸送方程式のモデルについて 小尾 晋之介 (慶應義塾大学) 原理原則を大切にしよう：流れの数値シミュレーションと乱流解析 森西 洋平 (名古屋工業大学) ドローン用高推力化ガイドの性能評価 加瀬 篤志 (富山大学) 風車研究における流れ計測 鎌田 泰成 (三重大学) 小型遠心ポンプのPIV計測 重光 亨 (徳島大学) 　｜　リンク一覧にもどる　｜

 

原理原則を大切にしよう：流れの数値シミュレーションと乱流解析

森西 洋平 名古屋工業大学

　本稿は2024年度日本機械学会年次大会（2024年9月8日～11日，愛媛大学）における筆者による基調講演（図１）を要約したものです．年次大会における基調講演と流体工学部門ニュースレター『流れ』への掲載機会を頂き，関係各位に深く感謝申し上げます．

　なお，基調講演は完全保存形差分スキームの開発に関する話題でしたが，差分スキームの具体形を記載するとニュースレターとしてはかなり冗長となってしまうので，以下では差分スキーム構築の要となる解析的な部分のみを記載します．完全保存形差分スキームの離散式の具体形に興味を持たれた方は関連論文（Morinishi et al.(1998), Morinishi (2010), Morinishi and Koga (2014)）をご覧下さい．

Fig.1 Keynote lecture in Mechanical Engineering Congress, 2024 Japan (MECJ-24)

１．はじめに

　タイトルにある原理原則とは，流れの支配方程式の解析的性質（移流項の型の互換性，保存特性），微分のライプニッツ則（積の微分の展開公式；，等），および相似性になります．これらを適切に表現する離散式を追及することで，筆者の代表研究である完全保存形差分スキームが開発されました．完全保存形保存差分スキームとは，輸送方程式の移流項に対する差分スキームで，元の輸送量に加え対応する自乗量も同時に保存するものであり，DNS (direct numerical simulation) やLES (large eddy simulation) による非定常乱流の数値計算に有効である事が知られています．

　自乗量保存特性の重要性を理解するため，非圧縮流れにおける移流方程式系（変数の輸送方程式と連続の式）を考えます．

ここでは方向の速度成分，は時間です．この移流方程式系では，非圧縮性流れに乗った変数が保存形で記述された輸送方程式に従って輸送されます．さらに，の輸送方程式に変数自身を乗じた後にライプニッツ則を用いて変形し連続の式を用いると自乗量の方程式が得られます．

この式は自乗量の保存則となっており，解析的な移流方程式系を解くと，輸送量に加えその自乗量 も保存される事を意味します．

　次に，移流方程式系の離散化を行います．

ここでと は差分法等による離散オペレータとします．しかし，この離散的な移流方程式系から導かれる自乗量の離散式を記述すると，離散オペレータ（差分等）では微分に対応するライプニッツ則が必ずしも成立しないため，一般的に自乗量保存形からのずれ（次式右辺の ）が生じる事になります．

これは，離散的な移流方程式系を解くと輸送量自体は保存されるが，対応する自乗量については一般的には保存されなくなる事を意味します．

　自乗量保存特性の重要性を明確に示すため，周期的流れ場について離散的な移流方程式系を解く場合の思考シミュレーションを考えます（図２）．離散的な移流方程式は保存形で記述されているので，離散式系が解ける限り，輸送量の平均値は保存されます．しかし，（生産的）の場合，時間進行に伴い変動が増幅され最後は発散に至ります．これは不安定な差分スキームの場合に対応します．一方，（散逸的）の場合，時間進行に伴い変動が減衰され最後は変動がほとんど無くなります．これは風上差分に対応し，滑らかな解が期待される場合（層流やRANSの数値計算）には有効ですが，乱流の非定常数値計算には不向きです．（中立）の場合のみ変動強度が維持され，乱れを含む流れ場の長時間積分を可能とするので，DNSやLESによる乱流の非定常数値計算に有効なものとなります．これを実現する移流項の差分スキームが完全保存形差分スキームに対応します．

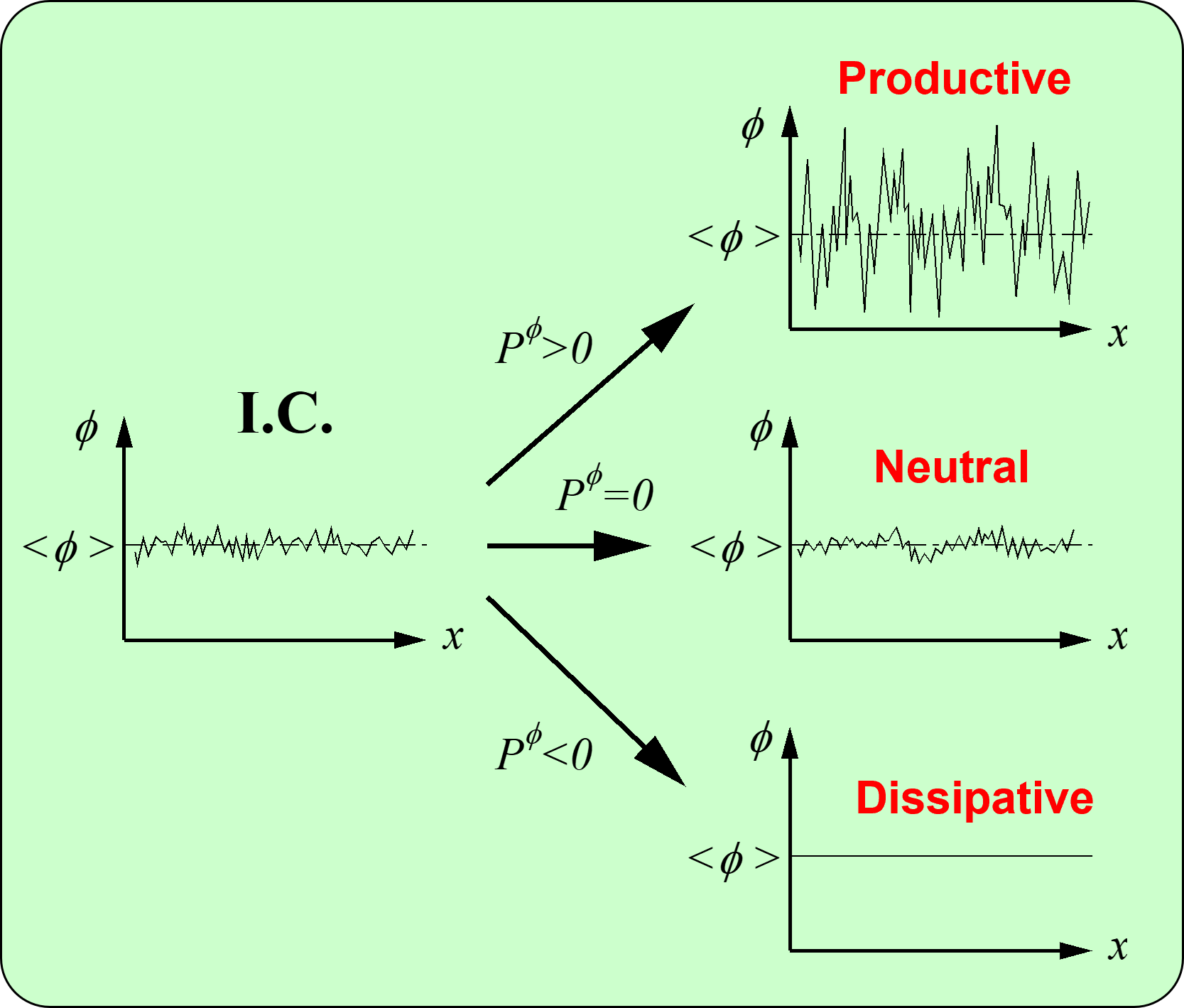
Fig.2 Periodic thought simulation

　以下では，非圧縮性流れ，圧縮性流れ，および移動変形格子それぞれに対する完全保存形差分スキームに関し，それらの開発の指針を与える移流項の型の互換性と保存特性（保存形，２次保存形），および相似性について簡単に紹介します．

２．非圧縮性流れに対する完全保存形差分スキーム

　非圧縮性流れのNS(Navier-Stokes)式の 方向の移流項を保存形(divergence型)，非保存形(advection型)，およびそれらの平均(skew-symmetric型)，で記述すると以下となります．

これらの移流項の型は，連続の式  が満足されると等価となります．

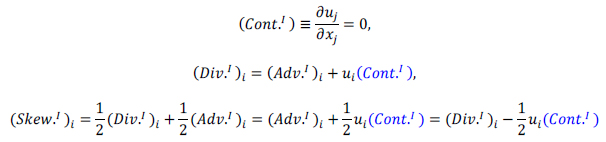
また，これらのうちdivergence型は先天的に(連続の式の成立に拘わらず)(1次)保存形，skew-symmetric型は先天的に2次保存形となります．

なお上式において指標は総和規約に従わないものとします．

　以上より解析的には，連続の式が成立すれば，これらの移流項の型は等価となり，また全てが完全保存形（１次かつ２次保存形）を与えるものとなります．このような移流項の型の互換性と保存特性は微分のライプニッツ則によって導出されます．

　移流項の離散式において，離散的な連続の式の成立により１次かつ２次保存形となるものを完全保存形差分スキームと呼びます．非圧縮性流れの数値計算に適したスタガード格子に対する空間２次精度の完全保存形差分スキームは，divergence型がHarlow and Welch (1965)，advection型が梶島(1994)，skew-symmetric型がPiacsek and Williams (1970) によって提案されております．スタガード格子での空間４次精度の完全保存形差分スキームの存在については1995年以前は世界的に疑問視されておりました．これに対し筆者は，離散オペレータとして任意のステンシル幅の差分，補間，およびパーマネント積を定義し，それらの離散オペレータ間に成立する恒等式（離散オペレータ間の互換性，ライプニッツ則の離散的表現，等）を整理することで，空間4次精度以上の完全保存形差分スキームの開発に成功しました(Morinishi(1995), Morinishi et al.(1998))．なおその後，時間空間完全離散式に対する２次精度の完全保存形差分スキームがHam et al. (2002) によって提案されております．

３．圧縮性流れに対する完全保存形差分スキーム

　圧縮性流れに対する連続の式（質量保存則） は次式で与えられます．

ここでは密度です．次に，圧縮性流れにおける変数の輸送方程式を考えます．

上式の左辺は保存形で記述されていますが，連続の式を用いることで非保存形にも書き換えられます．

これらの輸送方程式の左辺第２項が通常は移流項とみなされますが，本研究では左辺第１項の時間項も含めて圧縮性流れでの移流項の型を定義します．

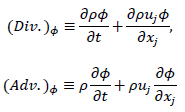
これらの型の定義より，連続の式 の成立による保存形(divergence型)と非保存形(advection型)の互換性が非圧縮性流れの場合と同様に表現されます．

一方，圧縮性流れに対するskew-symmetric型については，非圧縮性流れに対するものとの相似性を空間微分項のみに適用したものが提案されておりましたが（Feiereisen et al. (1981), Blaisdell et al. (1993), Morinishi et al. (2003)），それらは先天的な２次保存形とはなりません（擬skew-symmetric型）．筆者（Morinishi (2010)）は非圧縮性流れに対するものとの相似性を時間項も含めて考え，圧縮性流れに対する正しいskew-symmetric型を以下として提案しました．

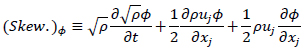
連続の式を通してのskew-symmetric型とdivergence型およびadvection型との互換性は非圧縮性流れに対するものと同様に次式で与えられます．

非圧縮性流れに対するものと同様に，これらもdivergence型が先天的に(1次)保存形，skew-symmetric型が先天的に2次保存形となります．

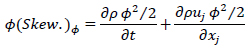
上記の正しいskew-symmetric型が示された事で，移流項の型の互換性と保存特性が非圧縮性流れに対するものと同等に議論できる様になり，それらを離散的に表現する事で圧縮性流れに対する完全保存形差分スキームが開発されました（Morinishi (2010)）．

４．移動変形格子に対する完全保存形差分スキーム

　ALE (arbitrary Lagrangian and Eulerian) タイプの移動変形格子に対する差分法では，物理空間から計算空間への写像が使用されます．その際，独立変数の変換に加え，移流項についてはおよびの置き換えが生じます．ここでは座標変換のヤコビアン，は格子の移動速度も考慮した反変速度成分です．この相似性を離散式へもそのまま適用することで，圧縮性流れに対する完全保存形差分スキームが移動変形格子に対するものへと拡張されました（Morinishi and Koga (2014)）．

５．まとめ

　完全保存形差分スキームは保存量と対応する自乗量を同時に離散的に保存する移流項の差分スキームで，DNSやLESによる乱流の非定常数値シミュレーションに有効です．完全保存形差分スキームは現在，非圧縮性流れ，圧縮性流れ，および移動変形格子で表現される流れに適用可能となっております．

　なお，ここで紹介した完全保存形差分スキームは，原理原則，つまり基礎式の解析的性質（移流項の型の互換性，保存特性），微分のライプニッツ則，および相似性，が離散式においても成立するように構成されたものとなります．

参考文献

[1]	Blaisdell, G.A., Mansour, N.N., Reynolds, W.C., Compressibility effects on the growth and structure of homogeneous turbulent shear flow, J. Fluid Mech., Vol. 256 (1993) 443-485.
[2]	Feiereisen, W.J. , Reynolds, W.C., Ferziger, J.H., Numerical simulation of compressible, homogeneous turbulent shear flow, Dep. Mechanical Engineering, Stanford Univ., Rep. TF-13, (1981).
[3]	Ham, F.E., Lien, F.S., Strong, A.B., A fully conservative second-order finite difference scheme for incompressible flow on nonuniform grids, J. Comput. Phys., Vol. 177 (2002) 117-133.
[4]	Harlow, F. H., Welch, J. E., Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface, The Physics of Fluids, Vol. 8 (1965), pp.2182-2189.
[5]	Kajishima, T., Conservation properties of finite difference method, Trans. JSME, Vol. 60, No. 574B (1994), pp.2058-2063 (in Japanese).
[6]	Morinishi, Y., Conservative properties of finite difference schemes for incompressible flow, CTR Annual Research Briefs 1995, Center for Turbulence Research, Stanford Univ./NASA Ames Research Center, (1996), pp.121-132.
[7]	Morinishi, Y., Lund, T. S., Vasilyev, O.V., Moin, P., Fully conservative higher order finite difference schemes for incompressible flow, J. Comput. Phys., Vol.143, (1998), pp.90-124.
[8]	Morinishi, Y., Tamano, S., Nakabayashi, K., A DNS algorithm using B-spline collocation method for compressible turbulent channel flow, Computers & Fluids, Vol. 32 (2003) 751-776.
[9]	Morinishi, Y., Skew-symmetric form of convective terms and fully conservative finite difference schemes for variable density low-Mach number flows, J. Comput. Phys., Vol. 229, (2010), pp.276-300.
[10]	Morinishi, Y., Koga, K., Skew-symmetric convection form and secondary conservative finite difference methods for moving grids, J. Comput. Phys., Vol. 257, (2014), pp.1081-1112.
[11]	Piacsek, S.A., Williams, G.P., Conservative properties of convection difference schemes, J. Comput. Phys., Vol. 6 (1970), 392-405.