流れ 2025年3月号 目次
― 特集テーマ:流体工学部門講演会(その2) ―
| リンク一覧にもどる | |
粘弾性流体乱流のラグランジュ統計
 |
 |
| 小井手 祐介 名古屋大学 |
後藤 晋 大阪大学 |
日本機械学会第102期流体工学部門講演会において,優秀講演表彰をいただきました.本稿では,講演内容である粘弾性流体乱流のラグランジュ統計について紹介します.
1.緒言
乱流中に微量の高分子を添加すると,乱流が劇的に抑制され,流動抵抗が大幅に低減することが知られています(1).高分子による乱流変調を説明する素過程として,乱流中の大小さまざまな渦と高分子との相互作用が重要であると考えられています(2).両者の相互作用は,高分子の伸長や緩和に応じて動的に変化します.乱流中での高分子の動力学や渦との相互作用を理解するためには,流れに乗った座標系から見た乱流のふるまい,すなわち,ラグランジュ的な性質が本質的に重要となります.そこで,本研究では,直接数値シミュレーション(DNS)を用いて高分子が乱流のラグランジュ的性質に及ぼす影響を調べました.
2.数値計算手法
本研究では,希薄高分子溶液の構成則としてFENE-Pモデルを用います.3方向に周期境界条件が課された周期箱乱流を対象とし,エネルギー注入率が一定となる外力で乱流を駆動します.具体的には,格子点数とし,ニュートン流体の場合のテイラー長レイノルズ数が約
となる乱流を対象とします.本稿では,希薄高分子溶液を特徴づけるパラメータのうち,高分子の緩和時間の影響に注目します.
ラグランジュ統計を調べるため,32768個の流体粒子を乱流中に一様に分散させ,トリリニア補間を用いて流体粒子の時間発展を計算します.それぞれの流体粒子の速度の時系列,すなわち,ラグランジュ速度をフーリエ変換し,アンサンブル平均を施すことで,パワースペクトル密度を評価します.
3.結果
高分子が添加された乱流のふるまいは,高分子の緩和時間に依存して顕著に変化します.Movie1に,緩和時間の異なる高分子が添加された乱流の様子を示します.具体的には,バンドパスフィルターを用いてスケール分解したエンストロフィーの等値面を示します.本稿では,高分子を添加する前のニュートン流体の乱流におけるコルモゴロフ時間
で
を無次元化したワイゼンベルグ数
と呼ばれる無次元量を用いて,
依存性を整理します.ニュートン流体の場合には,よく知られたように(3,4),波数
の渦が階層的に存在する様子が確認できます.一方,
の場合には,
の小スケールの渦がほとんど消失しており,
の場合には,
の中スケールの渦も抑制されています.乱流の空間構造の変化を定量的に調べるため,Fig. 1にエネルギースペクトル
を示します.ニュートン流体の場合には,コルモゴロフの相似仮説に基づくスケーリング則
に従う慣性領域が見られますが,
の増加に伴い
は高波数側から抑制され,先行研究(5)で報告されたスケーリング則
が現れます.
Movie 1 Isosurfaces of the bandpass-filtered enstrophy with the cutoff wavenumber (red),
(yellow), and
(cyan) for (a)
, (b)
, and (c)
.
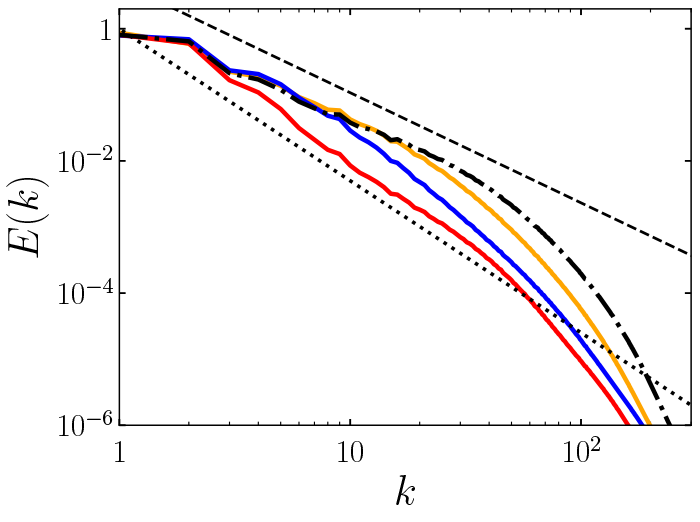
Figure 1 Energy spectrum of viscoelastic turbulent flows for
(orange),
(blue), and
(red). For comparison, the black dash-dotted line shows
of Newtonian fluids. The dashed and dotted lines show
and
, respectively.
次に,高分子によって空間構造が変調された乱流中でのラグランジュ速度の性質について調べます.Fig. 2に,ラグランジュ速度の成分
の時系列を示します.
が増加するにつれて,
の変動が穏やかになる傾向が見られます.より定量的に調べるため,Fig. 3に,ラグランジュ速度のパワースペクトル密度
を示します.ニュートン流体の場合には,コルモゴロフの相似仮説から予言されるスケーリング則
に従うことが知られています(6).一方,高分子が添加された場合は,
の増加に伴い高周波数側から順に抑制されますが,低周波成分はほとんどニュートン流体の場合のスペクトルと一致します.
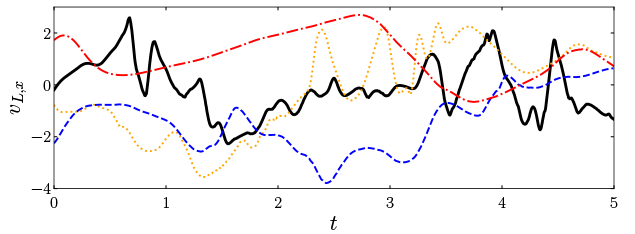
Figure 2 Lagrangian velocity in the
direction for
(black solid line),
(orange dotted line),
(blue dashed line), and
(red dash-dotted line).
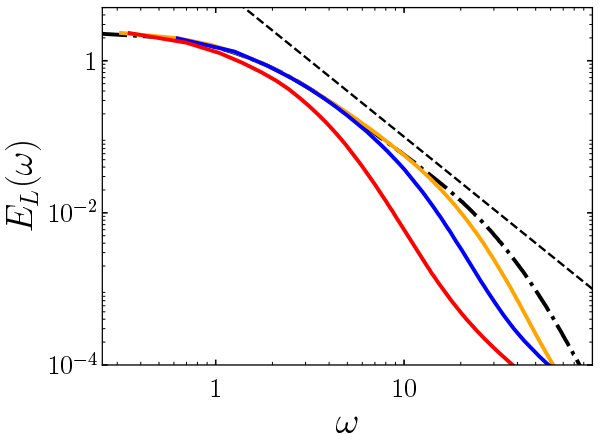
Figure 3 Power spectral density of the Lagrangian velocity
. The colors are the same as in Figure 1. For comparison, the black dash-dotted line shows
of Newtonian fluids. The dashed line shows
.
4.考察
高分子の緩和時間に依存したラグランジュ速度のパワースペクトル密度の変調機構を理解するため,ラグランジュ速度のスケール分解解析を行います.具体的には,バンドパスフィルターを用いて流速場をスケールごとに分解し,そのスケール分解された流速場を用いて,各スケールのラグランジュ速度への寄与を定義します(7).Fig. 4に,ニュートン流体の乱流の場合のスケール分解されたラグランジュ速度の成分
の時系列を示します.波数が小さい,すなわち,大きなスケールの渦ほど,振幅が大きく遅い変動を誘起します.このスケール分解を用いることで,それぞれのスケールの渦がラグランジュ速度のパワースペクトル密度に及ぼす影響を定量的に評価することができます.ここでは,Movie1の可視化に対応する3つのスケールのラグランジュ速度のパワースペクトル密度への寄与
をFig. 5に示します.
の場合に注目すると,Movie1に示した
のスケールの渦の抑制に伴い,
もニュートン流体に比べて減少しますが,
,
での
のふるまいはほとんど変化しません.
では,
のスケールの渦も抑制されるため,
での
の寄与もニュートン流体に比べて減少しますが,
の流れからの寄与は依然としてニュートン流体と同様のふるまいを示します.以上より,高分子による
の変調機構は以下のようにまとめられます.高分子の緩和時間が長くなると,乱流中の小スケールの渦から順に抑制され,その結果,小スケールの渦が作るラグランジュ速度の高周波成分が抑制されます.一方で,大スケールの流れはラグランジュ的な観点から見ても高分子の影響をほとんど受けないため,低周波成分はニュートン流体と同様の挙動を示します.
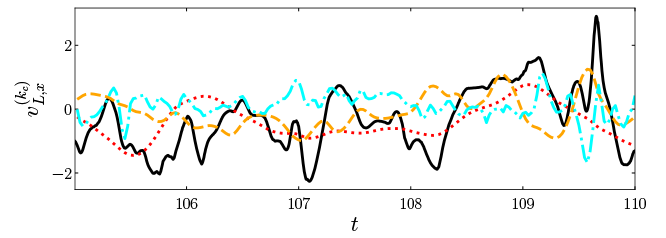
Figure 4 Bandpass-filtered Lagrangian velocity in the
direction for
(red dotted line),
(orange dashed line), and
(cyan dash-dotted line). The black solid line shows the raw Lagrangian velocity
in the
direction.
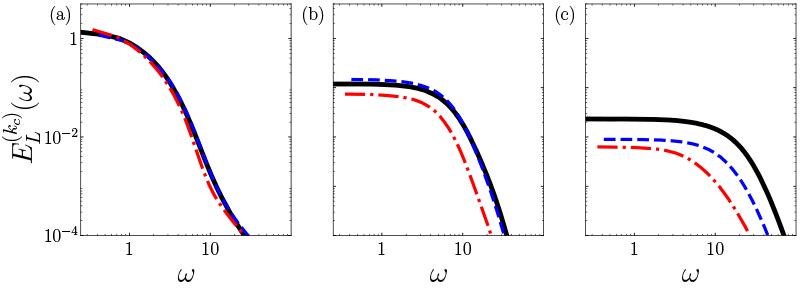
Figure 5 Power spectral density of the bandpass-filtered Lagrangian velocity
for (a)
, (b)
, and (c)
. Different colors correspond to different
: black,
; blue,
; red,
.
5.結言
高分子が乱流のラグランジュ的性質に及ぼす影響を明らかにするために,FENE-Pモデルを用いた3次元周期箱乱流のDNSを行い,ラグランジュ速度のパワースペクトル密度の緩和時間依存性を調べました.緩和時間の増加に伴い,
は高周波数領域から順に抑制されますが,低周波数領域ではニュートン流体とほとんど同じふるまいを示すことがわかりました.このようなスペクトルの変調機構を乱流中の渦の階層構造の観点から理解するため,ラグランジュ速度をスケールごとの寄与に分解しました.その結果,小スケールの渦は高分子によって減衰するため,ラグランジュ速度の高周波成分は減衰するのに対し,大スケール渦はラグランジュ的な観点から見ても高分子の影響をほとんど受けないため低周波成分に変調が見られないことがわかりました.
6.謝辞
末筆ながら,優秀講演表彰の審査にご尽力いただきました選考委員会の皆様ならびに日本機械学会流体工学部門の皆様に,心より御礼申し上げます.本研究は,JSPS科研費(24KJ0109),核融合科学研究所一般共同研究(NIFS22KISS010)の援助のもと行いました.

