流れ 2025年3月号 目次
― 特集テーマ：流体工学部門講演会（その2） ―
｜ リンク一覧にもどる ｜ |
移動壁面下に発達する乱流境界層における気泡群の運動と抵抗低減効果
 |
| 森 樹， 堀本 康文， 朴 炫珍， 田坂 裕司， 村井 祐一 （北海道大学） |
この度，日本機械学会第102期流体工学部門講演会において優秀講演表彰を賜りました．改めまして，選考委員会および日本機械学会の皆様に深く感謝申し上げます．本ニュースレターでは，当該講演会で発表いたしました研究内容についてご報告いたします．
1．緒言
乱流境界層内への気泡注入により壁面に作用する摩擦抵抗を低減できることが広く知られています(1)．この手法は空気潤滑法と称され，従来燃料船の運航効率向上に寄与する技術として注目されています．実船実験(2,3)では，正味約10％の省エネルギー効果が報告されており，さらなる抵抗低減効果の向上のため，注入気泡が乱流境界層に及ぼす影響の予測および制御手法の開発が急務となっています．
これまで，実船に近い条件下での検証を目的として，大型の水槽における模型船曳航実験(4)が実施されてきましたが，これらの実験は莫大なコストおよび時間を要するため，より効率的に乱流境界層における空気潤滑効果を評価できる実験室スケールの手法の確立が強く求められています．実験室における研究は，継続的かつ詳細な計測が可能であり，よく制御された条件下で系統的なデータ取得ができる点で，摩擦抵抗低減メカニズムの解明に大きな利点をもたらします．
しかしながら，これまでの多くの実験室スケールの研究は水平チャネル流を対象としており，実船に適用する際には以下の点に留意する必要があります（図1）．第一に，平板に挟まれたチャネル流では一定の流下距離を経過すると乱流境界層が発達しなくなるのに対し，船底の乱流境界層は空間的に発展し続けます．第二に，チャネル流では流下方向に圧力勾配が存在するのに対し，船底ではゼロ圧力勾配下で境界層が発達します．第三に，船底とチャネルでは壁面垂直方向の速度勾配が逆転しており，これにともない気泡に働く揚力の向きも反転します．これらの違いは，水と比べ密度の極めて低い気泡の運動に大きな影響を及ぼします．
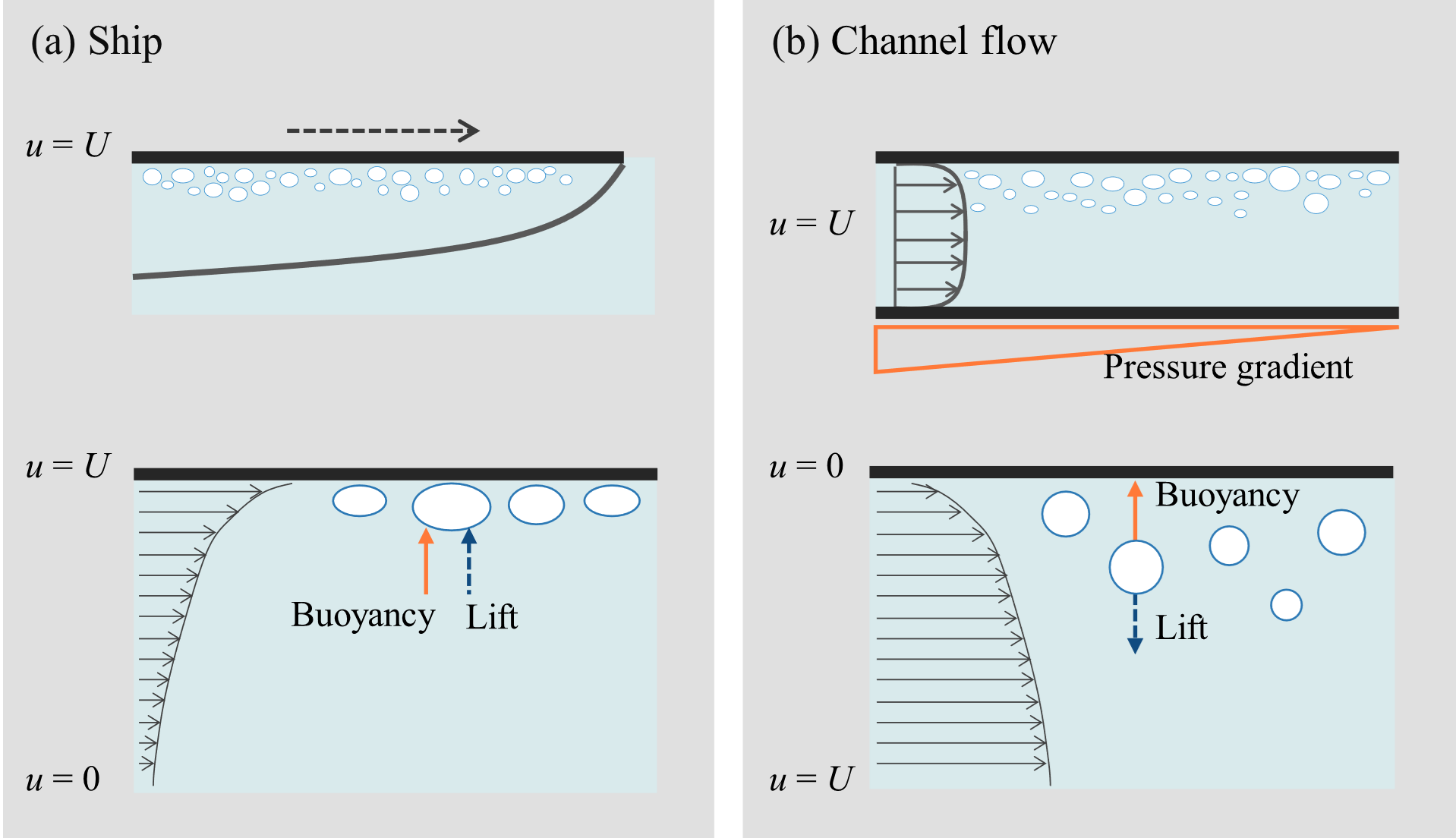
【Figure 1 Conditions (a) beneath a ship and (b) in horizontal channel flow.】
以上の背景を踏まえ，我々は移動壁面下の片側平板境界層を再現可能な新たな実験系（図2）を構築しました(5)．本実験系では，静止した水槽内で水平にベルトを動かすことで実際の船舶に近い条件を再現しています．本研究では，この新たな実験系を用いて空気注入量および壁面速度を系統的に変化させ，各条件での空気潤滑効果を評価するとともに，粒子追跡流速計測法（PTV）を用いて気泡注入が乱流統計量に与える影響を解析しました．
【Figure 2 Photograph of the experimental system used in this study.】
2．実験装置
図3に実験装置の概要を示します．本装置は，透明アクリル樹脂製の水槽，ポリウレタン製のベルト駆動部，および空気注入用の配管系から構成されています．
.png)
.png)
【Figure 3 Schematics of (a) the present experimental facility and (b) its side view. The x, y, and z coordinates are aligned in the streamwise, wall-normal and spanwise directions, respectively.】
下流側の駆動プーリーをステッピングモーター（ARM66AC-PS25，オリエンタルモーター）に接続することでベルトの移動速度Uを制御します．これにより，ベルトの下には乱流境界層が維持されます（動画1）．また，トルクメーター（UTMⅢ-10Nm，ユニパルス）を用いて，ベルト駆動時にモーターにかかるトルクを計測することで，ベルトに作用する摩擦抵抗を評価できることもこの実験系の特長です．
【Video 1 Turbulent boundary layer developed beneath a moving belt visualized by using light-reflective flakes.】
注入する気体は，エアコンプレッサー（AK-HL1270E3，マックス）から供給される圧縮空気であり，ベルトの上流端から195 mm，水深5 mmの位置に，スパン方向に一列に配置された外形1.2 mm，内径0.9 mmの管から放出されます（動画2）．また注入する空気の流量Qは，流量計（QFS-200，東京メータ）により計測しています．
【Video 2 A video showing the bubble injection area taken from below.】
3．トルクの計測結果に基づく抵抗低減効果の評価
トルクメーターで計測される各種の抵抗は，摩擦抵抗以外は気泡注入の影響を受けません．そのため，気泡注入の有無における平均トルクの差から，気泡注入位置より下流側全体の摩擦抵抗低減量∆Rを求めることができます．
計測手法は次のとおりです．各条件で，気泡注入前の単相流状態で2回，気泡注入開始後の気液二相流状態で4回，気泡注入終了後の単相流状態で2回のトルク計測を行い，それぞれの平均値の差から気泡注入による変動を算出しました．これを1セットとし，再現性の確認のため各条件で3セットの計測を実施しました．
単相流および二相流それぞれの4回の平均値をTsおよびTtとし，ベルト駆動軸側のタイミングプーリーに対するモーター軸側のタイミングプーリーに対する歯数比rとベルト駆動軸のプーリー直径Dを用いると，抵抗低減量∆Rは次式で定義できます．
 |
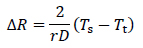(1) |
また，気泡存在領域における単相状態での摩擦抵抗Rsを用いることで，抵抗低減率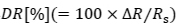
を評価できます．なお，Rsは装置の特性上トルクの値から直接算出できないため，PTVの計測結果から得た運動量厚さの空間的発達を表す式と，von Kármánの積分方程式を用いて値を見積もりました．
図4に各条件での気泡の様子を，図5に各条件でのDRを示します．図中のtaはta = Q / UW（Wはベルトの幅）で定義される公称気膜厚さです．結果として，壁面移動速度にかかわらず，空気注入量が多いほどDRが高くなる傾向が確認されました．気泡の様子とDRの値を照らし合わせると，気膜が確認されたU = 1.20 m/s，Q = 2.08 × 10-4 m3/s（ta = 0.92 mm）とU = 1.20 m/s，Q = 2.50 × 10-4 m3/s（ta = 1.11 mm）の条件ではDRが10%から25%の高い値となっていることが分かります．一方，主に直径20 mm以下の気泡が観測されたその他の条件ではDRが0%から13%の範囲となりました．これらの結果から，空気注入量が特に少ない条件を除けば，空気注入は常に摩擦抵抗の低減に寄与し，その効果は気泡径分布などの気泡特性に依存することが示されました．
【Figure 4 Photographs of the injected air bubble in 748 mm ≤ x ≤ 932 mm recorded
through the bottom of the water tank.
】
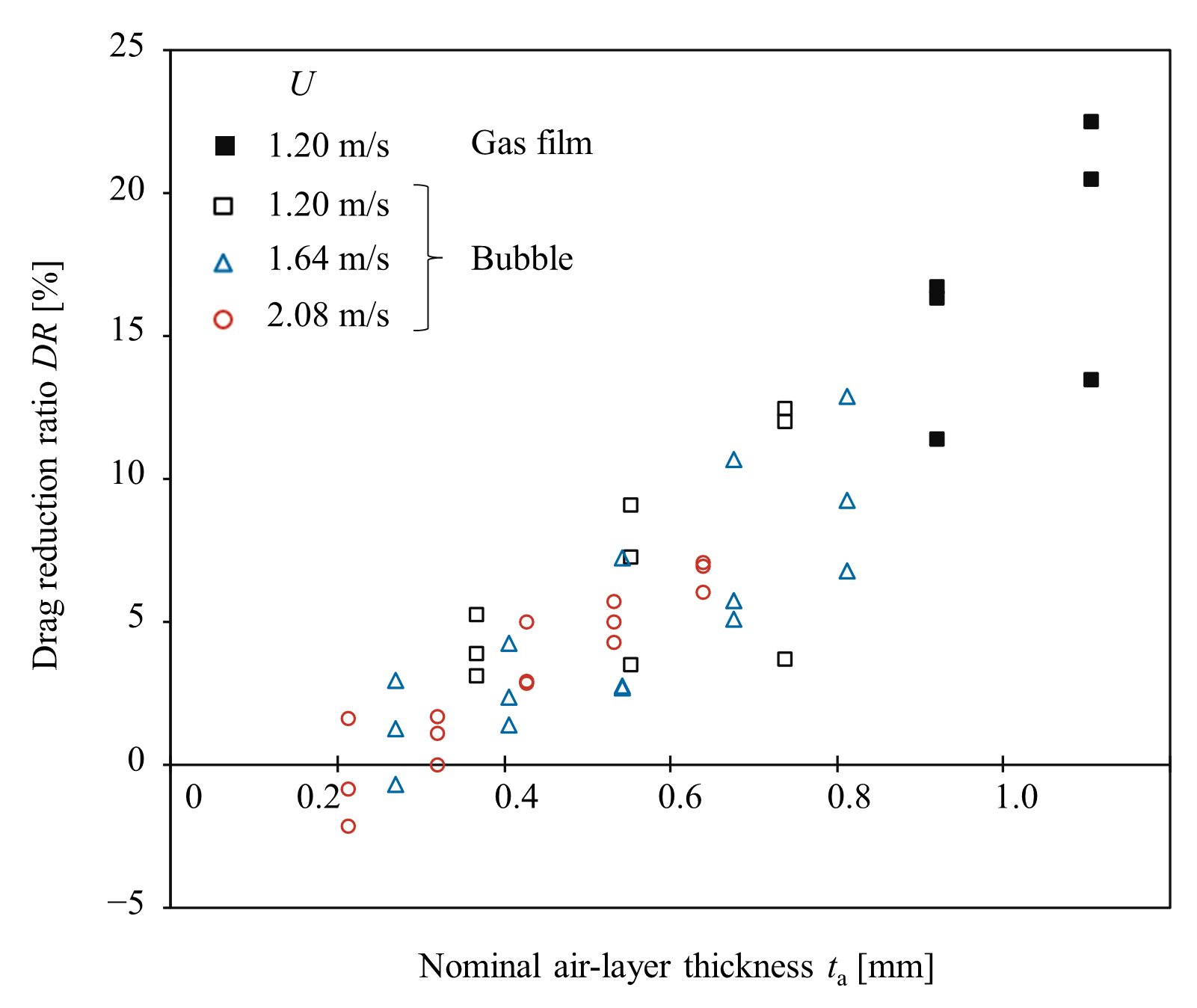
【Figure 5 Drag reduction ratio for each condition.】
4．気泡注入による速度場の変化
壁面移動速度と空気注入量を系統的に変化させ，各条件においてPTVにより速度場を得ました．図6および図7は，得られた速度場を基に算出した，ベルトに対するy方向の相対平均速度分布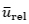
およびReynoldsせん断応力
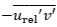の分布を示しています．なおReynoldsせん断応力の値は，先述のvon Kármánの積分方程式を用いて算出した，壁面せん断応力から求めた単相状態での摩擦速度
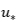により規格化しています．
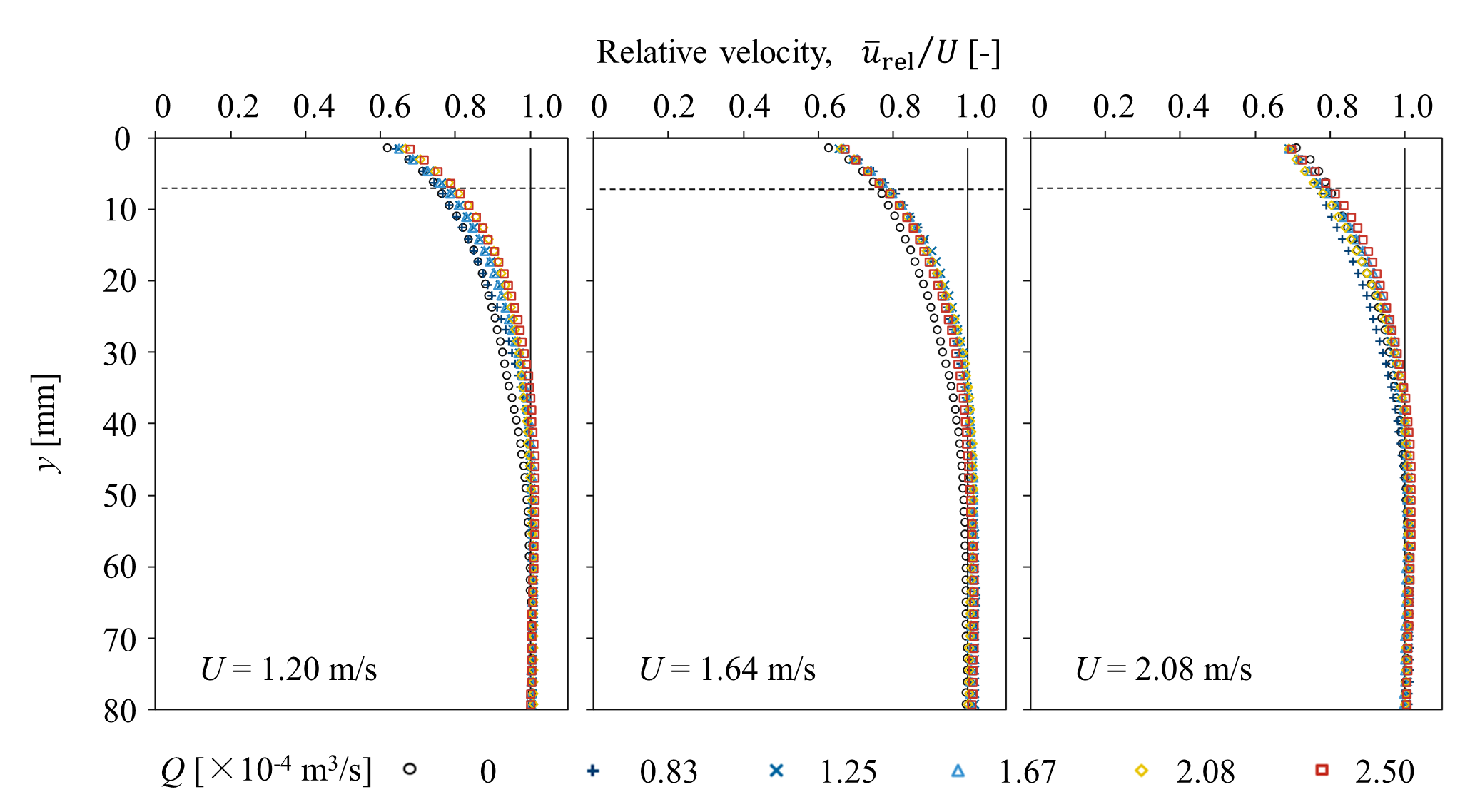
【Figure 6 Mean velocity profile relative to the belt for each air injection rate and belt speed. The solid line in the graph represents the belt speed, while the dashed line indicates the approximate upper boundary of the region where bubbles are present.】
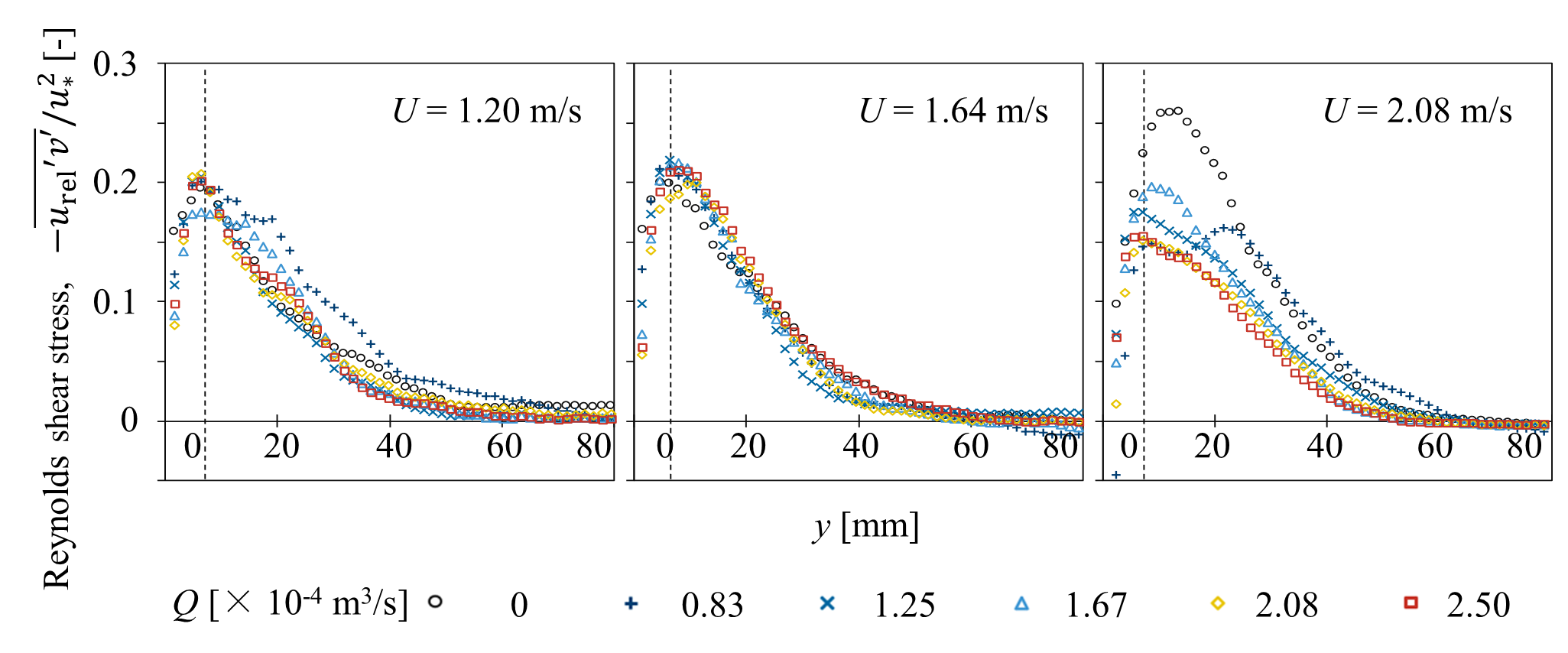
【Figure 7 Reynolds shear stress for each air injection rate and belt speed. Reynolds shear stress is normalized by the wall variables of the single-phase flow. The dashed line in the graph represents the approximate upper boundary of the region where bubbles are present.】
得られた結果をもとに，気泡注入の有無が速度場に与える影響を検討しました．壁面移動速度が比較的低速であるU ＝ 1.20 m/sおよびU ＝ 1.64 m/sの条件では，気泡注入時に相対平均流速分布が増加する傾向が確認されました．これに対し，U ＝ 2.08 m/sの条件では，気泡の有無による顕著な変化は見受けられませんでした．一方，Reynoldsせん断応力の分布については，壁面移動速度が最も高速であるU ＝ 2.08 m/sの条件において，気泡注入により全体的に値が減少することが観察されました．これに対し，U ＝ 1.20 m/sおよびU ＝ 1.64 m/sの条件では，気泡の有無によるReynoldsせん断応力の分布に明確な差は認められませんでした．
これらの結果は，気泡が乱流構造に及ぼす影響が壁面移動速度の条件により異なることを示唆しています．具体的には，U ＝ 1.20 m/sおよびU ＝ 1.64 m/sの条件では，液相における壁面からの運動量輸送が減少していないにもかかわらず，前節で示した抵抗低減効果が確認されました．この結果は，気液二相流体としての見かけの密度低下や接触面積の減少が支配的なメカニズムである可能性を示唆しています．一方で，U ＝ 2.08 m/sの条件では，壁面からの運動量輸送が減少していることが観察され，気泡が乱流構造に直接的な影響を及ぼしている可能性があると考えられます．以上の議論から，気泡注入による効果は，壁面移動速度の違いに応じて異なるメカニズムにより現れると考えられます．
5．結言
本研究では，新たに構築した実験室スケールの装置を用いて，片側乱流境界層内での気泡注入と乱流構造の関係を詳細に評価しました．トルク計測およびPTV解析の結果，気泡注入が摩擦抵抗の低減に寄与することが確認され，その効果が壁面移動速度および空気注入量に依存することが明らかとなりました．特に，高速条件下では，気泡が乱流構造に直接影響を及ぼしていると考えられます．
これらの成果は，空気潤滑法の基礎的理解を深めるとともに，実船における摩擦抵抗低減の実現に向けた今後の研究に重要な示唆を与えるものと考えられます．また，気泡径，気泡注入量，および壁面移動速度が乱流構造や摩擦抵抗低減効果に与える影響を定量的に評価する手法を確立できた点は，今後の研究の基盤となる成果です． 今後は，速度場の統計的解析だけでなく，気泡通過に伴う局所的な流れの変化を定量的に評価し，気泡注入による摩擦抵抗低減メカニズムをより包括的に解明することを目指します．