流れ　2025年3月号　目次

―　特集テーマ：流体工学部門講演会（その2）　― 巻頭言 （朴，松田，洪） 光ファイバーを用いた液膜流の膜厚分布計測法の検討 中野 幸佑，水嶋 祐基（静岡大学） 粘弾性流体乱流のラグランジュ統計 小井手 祐介（名古屋大学），後藤 晋（大阪大学） 電場印加型絞り流路を用いたセルロース・銀ナノ粒子複合繊維創製 平 和佳菜， 金子 泰， 高奈 秀匡（東北大学） NACA0018翼型に基づくブレードの翼型面方向がV形垂直軸風車の出力特性に与える影響 大井 翔生，馬場先 貴紀，櫻井 遼，河野 孝昭，木綿 隆弘，小松 信義（金沢大学） 移動壁面下に発達する乱流境界層における気泡群の運動と抵抗低減効果 森 樹，堀本 康文，朴 炫珍，田坂 裕司，村井 祐一（北海道大学） 　｜　リンク一覧にもどる　｜

 

電場印加型絞り流路を用いたセルロース・銀ナノ粒子複合繊維創製

大井 翔生， 馬場先 貴紀， 櫻井 遼， 河野 孝昭， 木綿 隆弘， 小松 信義 （金沢大学）

1.　緒言

　この度は，日本機械学会第102期流体工学部門講演会にて，栄えある優秀講演表彰をいただいた．この場を借りて日本機械学会の皆様および選考委員会の皆様に御礼申し上げる．本ニュースレターでは，講演発表内容について紹介する．

　浮体式洋上風力発電の普及には，風車の低コスト化に加えて，浮体構造物の低コスト化が大きな課題である．現在浮体式風車として主流である水平軸風車は，発電機等の重量物が風車上部に設置され，さらにロータに作用する風荷重がタワー上部に作用するため設計転倒モーメントが大きく，浮体構造物の低コスト化には難しさがある．一方，垂直軸風車は，発電機等の重量物が下方に設置され，さらにロータに作用する風荷重がシャフト高さ方向に広く分布するため設計転倒モーメントを小さくできることから，浮体式洋上風力発電の浮体構造物の低コスト化の上で利点がある⁽¹⁾．高効率な揚力型垂直軸風車であるダリウス風車のロータ形状として代表的なトロポスキン形は，翼のピッチ角制御による高効率化や強風時の対応が難しい．また，H 形は，アームの空力抵抗によるトルク損失が大きいという欠点がある．研究事例は非常に限られているが，V形のロータ形状は，アームやアームを支持する部品を必要としないため，トロポスキン形やH 形に比べて風車の低コスト化の上で利点があるとともに，ピッチ角制御により強風時の風荷重を低減できるため，設計転倒モーメントを小さくすることが可能となり浮体構造物の低コスト化の上でも利点を有する．また，アームによるトルク損失も発生せず，ピッチ角制御も可能であり，高効率化の余地が大きい．しかし，V形垂直軸風車の研究事例は非常に限られている．数少ない研究事例の一つであるRahmanらの研究では，翼の各高さにおける翼弦線の前縁から25%位置をつないだ直線とNACA翼型面が直交しており，翼の水平断面が高い翼性能の翼型になっていない可能性がある⁽²⁾．そこで本報では，V形垂直軸風車の翼のピッチ角をロータ回転中に一定とした場合に，NACA0018翼型の面方向が45°異なる2種類の翼のコーニング角および翼型面方向の違いが風車出力特性に与える影響について，風洞実験と数値流体力学(CFD)解析により調べた結果を報告する．

2.　供試風車

　図1，表1に本研究で対象とするV形垂直軸風車の形状と寸法を示す．翼枚数は2枚，翼スパン長さは0.35 m，翼先端部における翼弦長は0.07 m，翼下端部における翼弦長は0.10 mである．各高さにおける翼弦線の前縁から25%位置をつないだ直線を翼根回転軸，翼根回転軸と水平面のなす角度をコーニング角βと呼称する．翼型面上の，翼弦線と翼回転軌道接線のなす角度である取り付け角α（図2）は，翼のすべての高さにおいてα = 4° である．図3に翼の形状を示す．通常翼は，翼型面が翼根回転軸に垂直となっており，傾斜翼は，β = 45°のとき翼型面が水平面と平行となっている．翼型は，翼先端から中間部にかけては NACA0018，中間部から翼下端部にかけては強度を高めるためにNACA0050へ滑らかにシフトしている．風車の直径D は，β = 45°のときにD = 0.8 mであり，β = 40°では約0.06 m増加し，β = 50°では約0.07 m減少する．風車の回転方向は風車上方から見て反時計回りであり，アジマス角θを図4のように定義する．

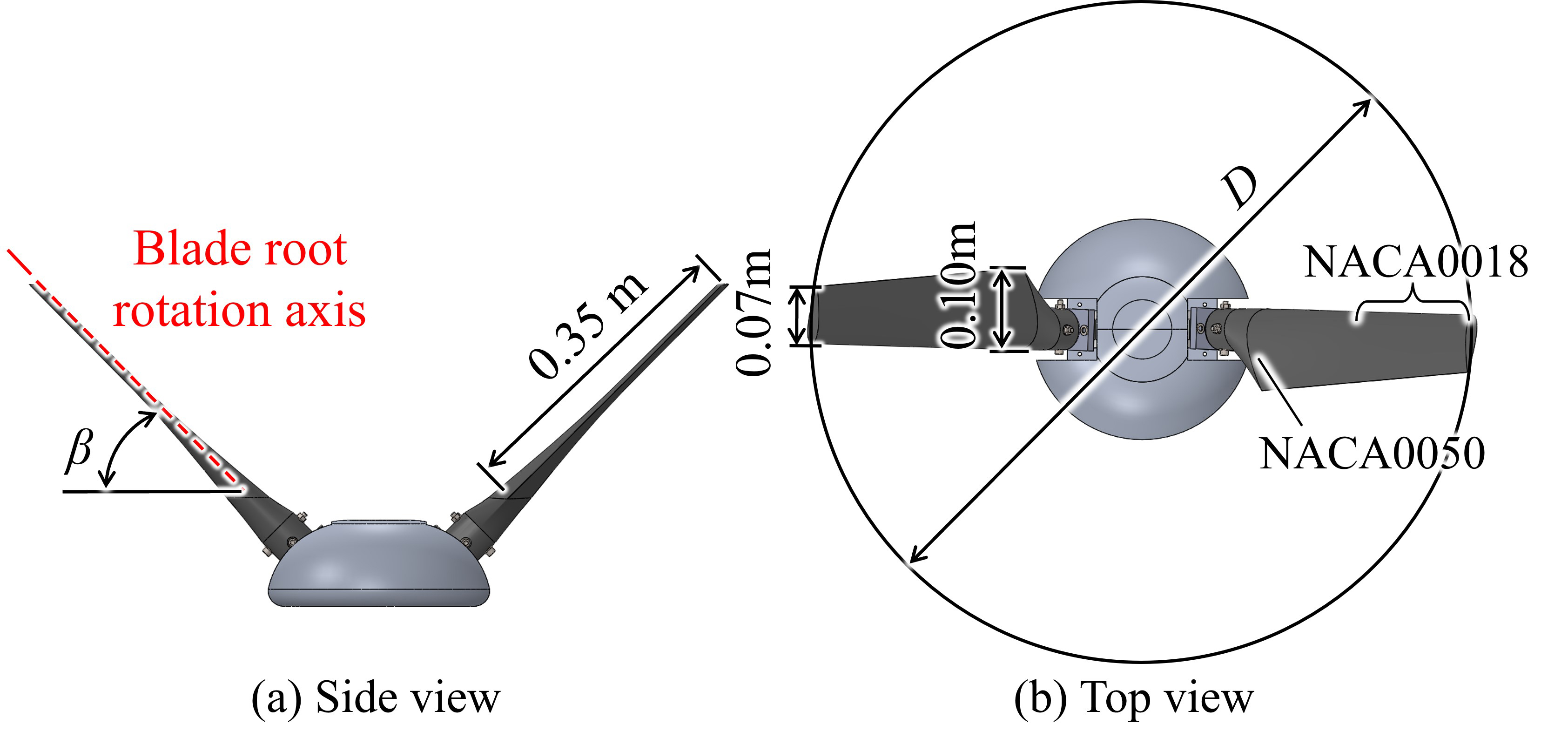
Fig. 1　Designed model of V-VAWT with 2 blades

Table 1  Coning angle and diameter of V-VAWT

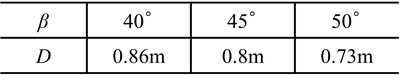
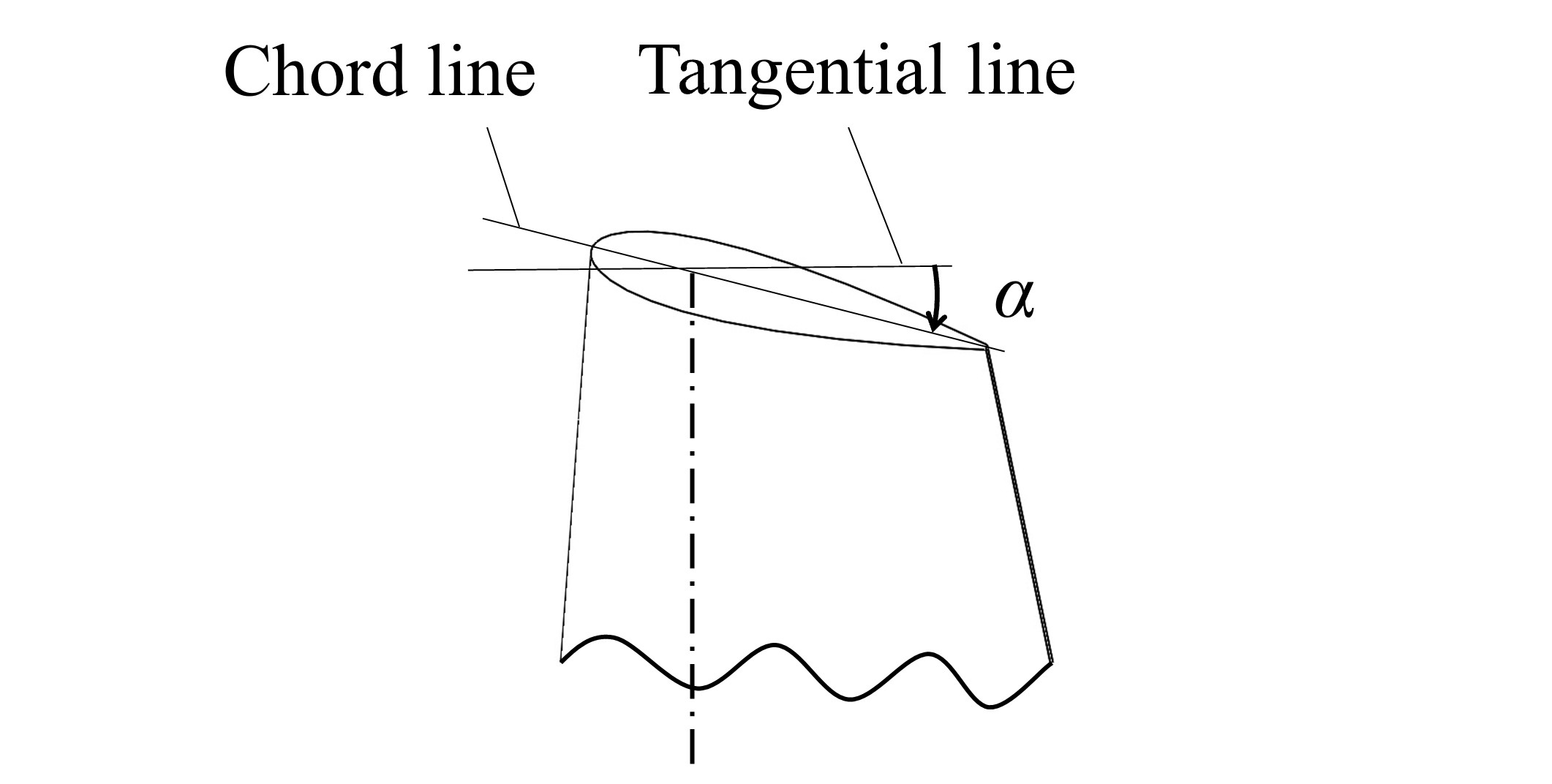
Fig. 2　Definition of blade’ setting angle α

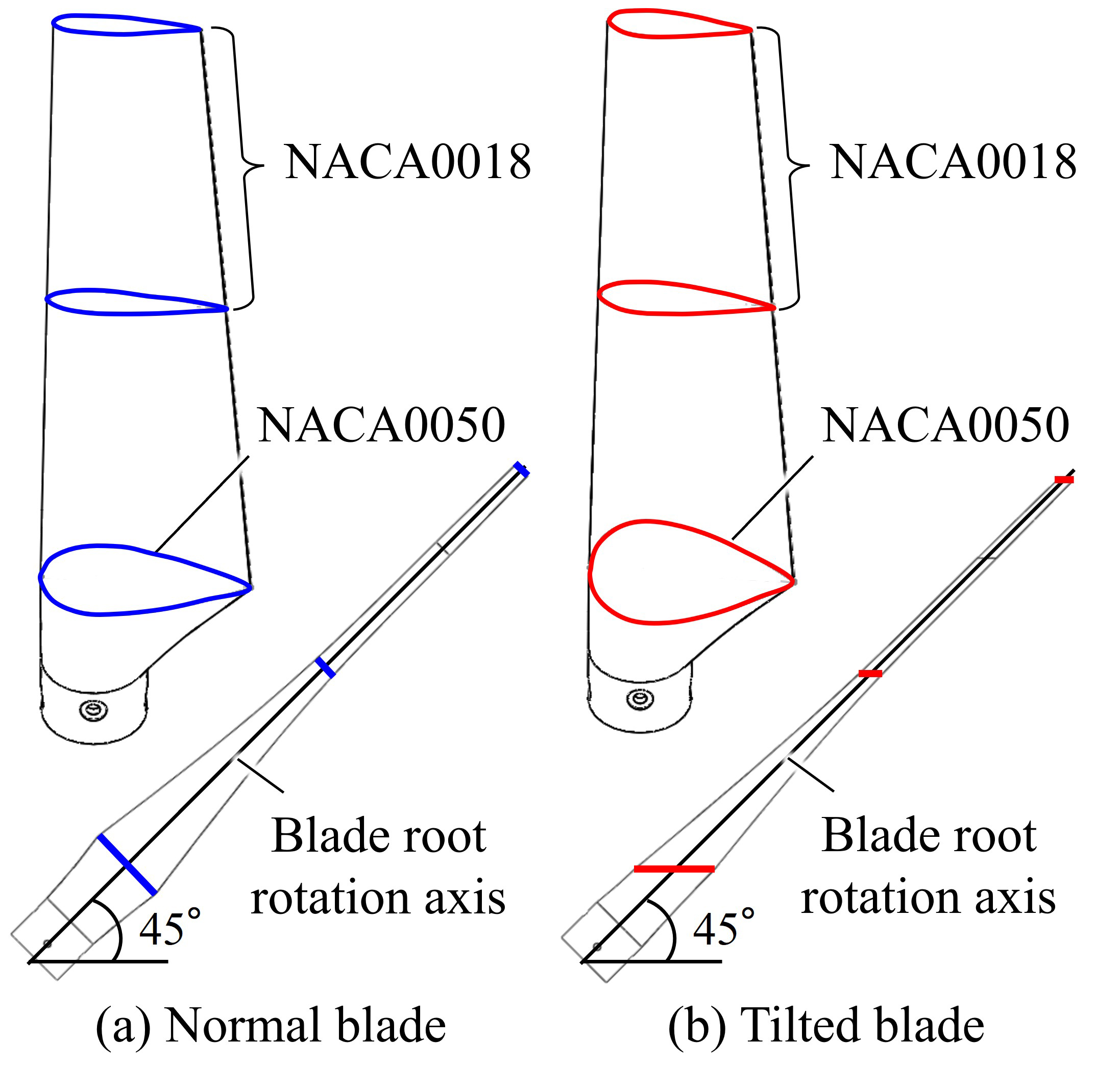
Fig. 3　Shape of blades

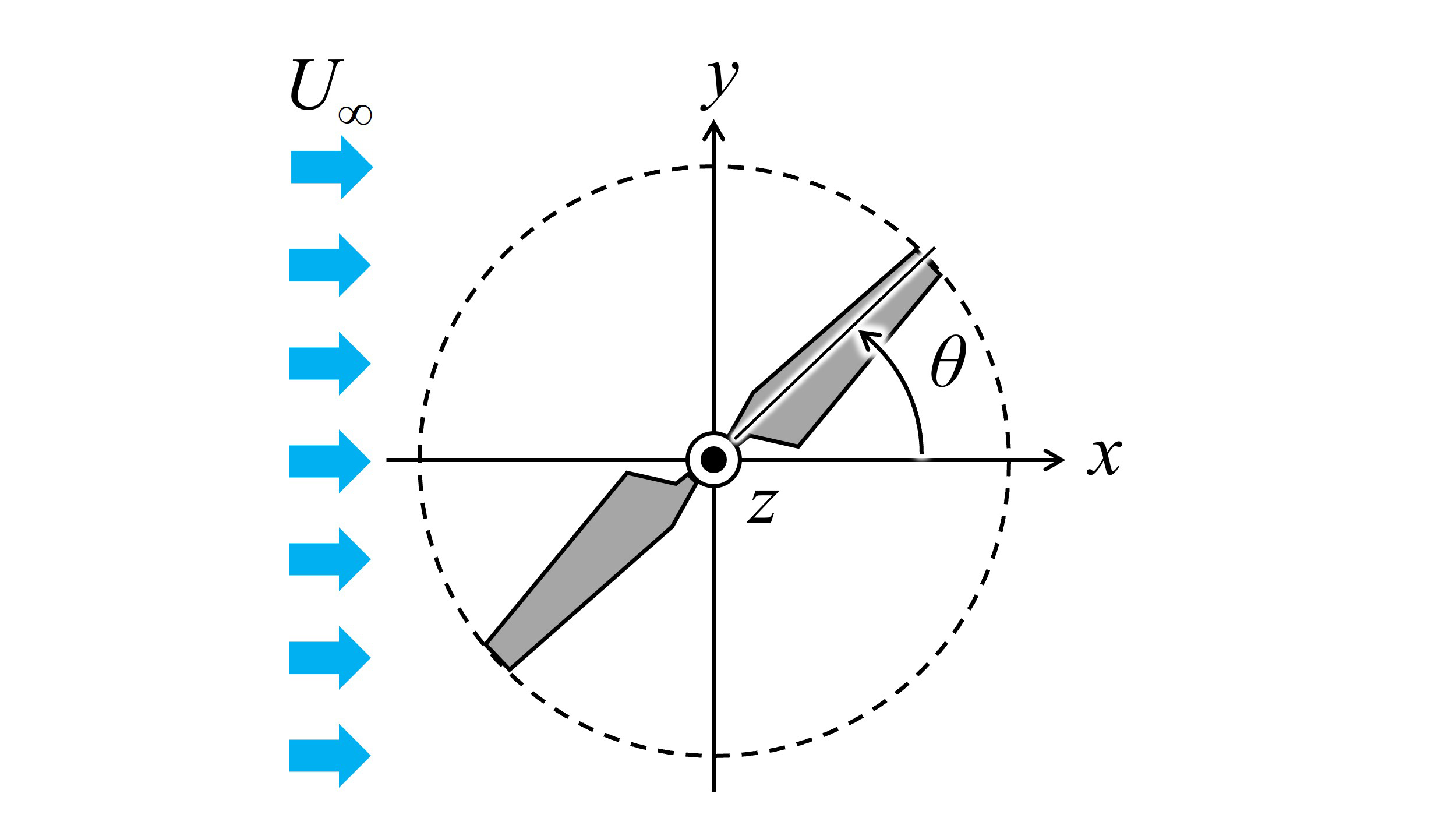
Fig. 4　xyz coordinates and azimuth angle θ(Top view)

3.　実験手法

　図5に実験装置の概略を示す．実験にはノズル断面寸法が1250 mm×1250 mmであり，吹き出し口と長さ2000 mmの開放型測定部を有する回流型風洞を用いる．測定部内には，吹き出し口からx = 1000 mmの位置に供試風車を設置する．風洞では一様流を生成し，吹き出し口からx = −4000 mmの位置にある超音波風速計での基準風速がU_∞ = 7 m/s となるように軸流ファンの回転数を制御する．風車の回転数nをDCモータ（オリエンタルモーター，BLVM640N-A）により制御し，各周速比 λ（= Dω / 2 U_∞）におけるトルクQについてωが増加中の場合と減少中の場合でそれぞれ計2回計測する．ここで，ω（= 2πn / 60）はロータ角速度である．風車の出力係数C_P（= Qω / 0.5ρA U_∞³）の算出の際に用いる代表面積Aは，上流側から見たロータ受風見つけ面積が最大となるβ = 45°における値であり，(D − 0.35cosβ)(0.35sinβ) = 0.137 m²である．ここで，ρは空気密度である．また，C_Pの算出においては，翼のみを取り外した状態で計測したベアリング等の機械損失を考慮する．

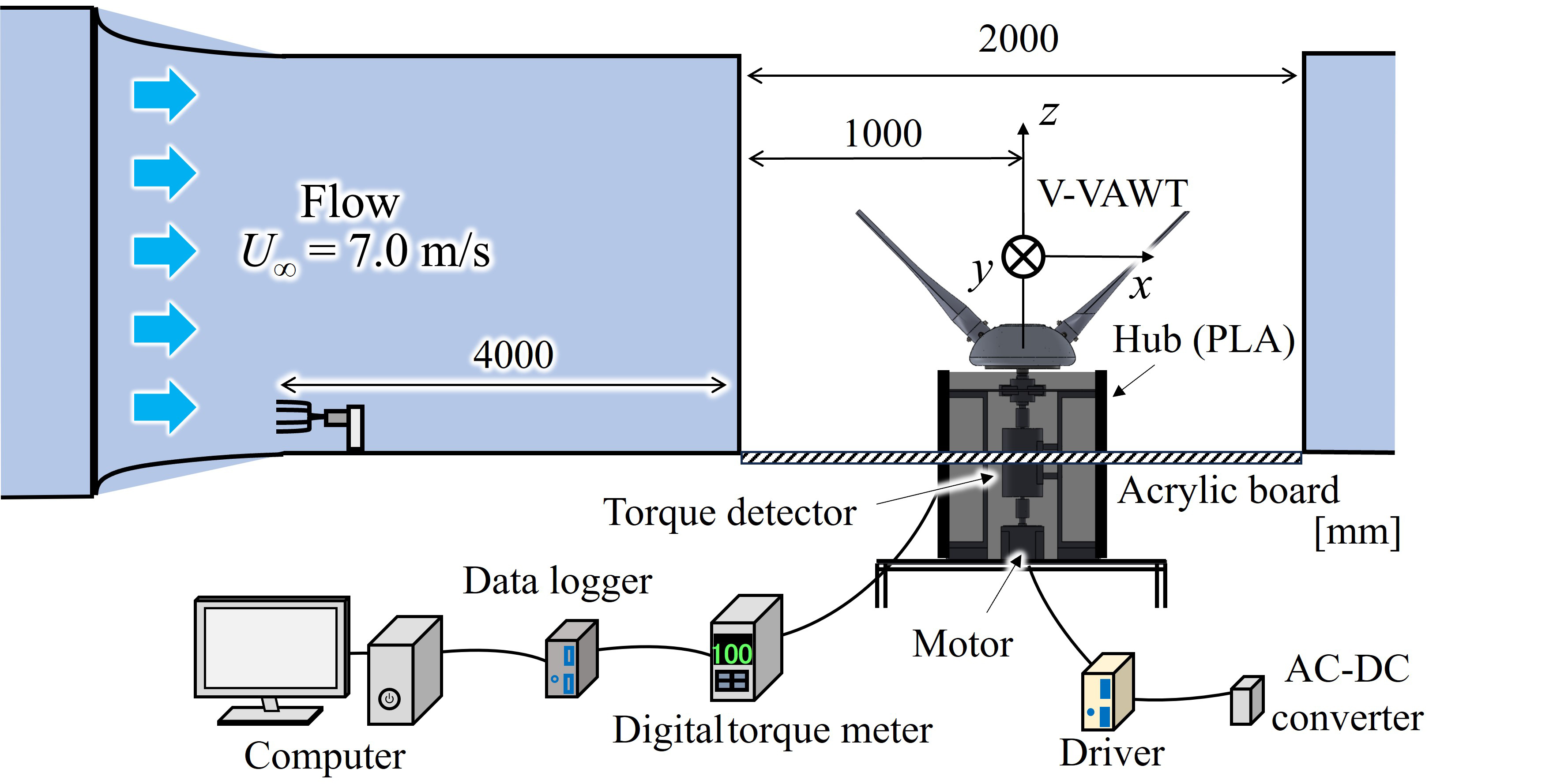
Fig. 5　Experimental setup

4.　CFD解析手法

　翼枚数2枚，β ＝ 45°のV形垂直軸風車の3次元形状を解析対象とする．図6に解析に用いる解析格子とその境界条件を示す．解析格子は，静止領域と回転領域で構成されている．総セル数は通常翼，傾斜翼ともに約3,000万である．流れ場は3次元，非定常，非圧縮，粘性と仮定し，作動流体は15℃の空気とする．支配方程式にはフィルター操作を施した連続の式とNavier-Stokes方程式，Large-Eddy SimulationのサブグリッドスケールモデルにはWALEモデルを用いる．数値解析ソフトウェアにはOpenFOAM5.0とOpenFOAMv2206を使用する．

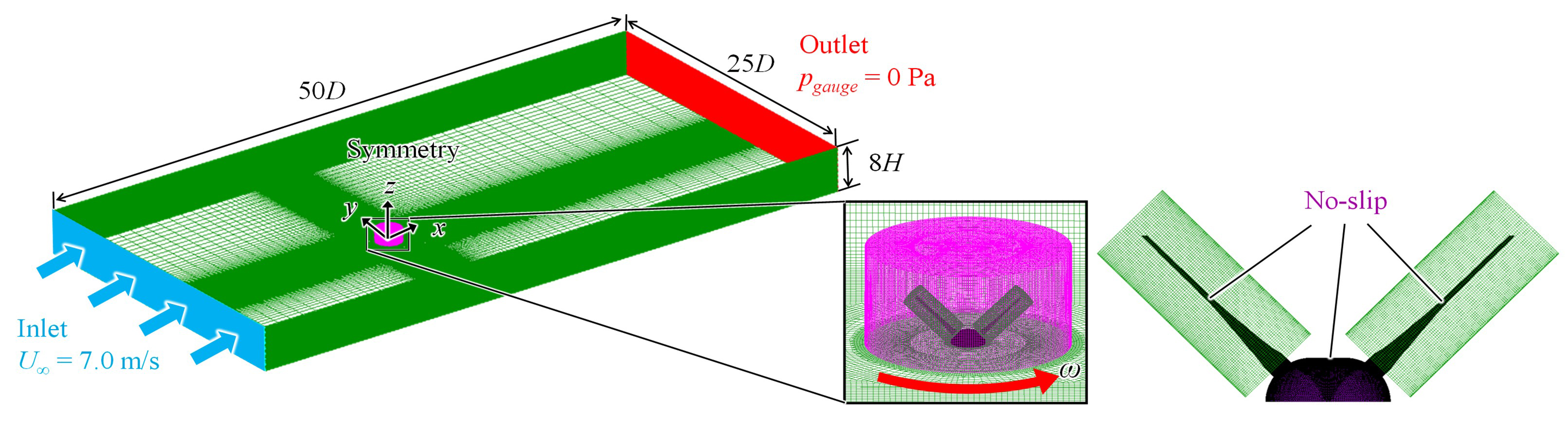
Fig. 6　Computational domain and boundary conditions

　境界条件には，流入境界に一様流速7.0 m/s，流出境界にゲージ圧0 Pa，上下左右の側面境界に対称境界条件を課し，風車の固体表面にはNo-slip条件を設定する．周速比は通常翼がλ = 3.1，傾斜翼がλ = 3.8，時間刻み幅はロータが0.05°回転する時間である．

5.　実験結果および考察

　図7に各翼形状において，βを変化させた場合のC_P –λ曲線を示す．いずれの翼形状においてもβ = 50°で出力係数が最大となっており，通常翼はλ = 3.2のときC_{P_max} = 0.23，傾斜翼はλ = 3.7のときC_{P_max} = 0.28である．β = 50°で出力係数が最大となった要因として，ロータの回転に伴う遠心力により，翼がロータ半径外側方向へしなり，受風面積が最大値に近づいているとともに，傾斜翼においては翼の水平断面が高い揚力を発生するNACA0018翼型に近づいていることが考えられる．図8に示すように，最適周速比付近でβ = 50°の翼がしなり，λ = 0におけるβ = 45°の形状に近づいていることを，高速度カメラで撮影した画像を重ね合わせて確認している．

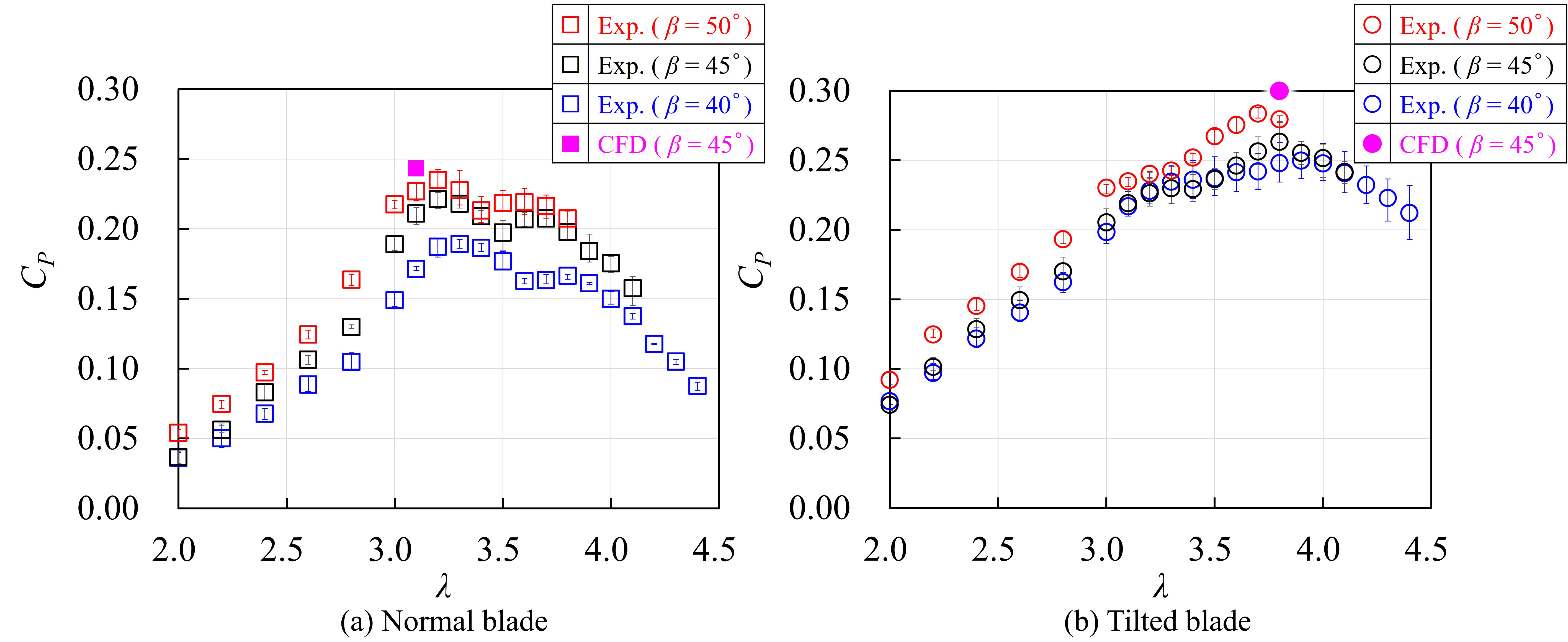
Fig. 7　C_P –λ curve

Fig. 8　Photos of V-VAWT(θ = 0°,180°)

6.　CFD解析結果および考察

　図9に，翼一枚のトルク係数C_Qb1 (= 4Q_b1­­/ρAU_∞²D)とアジマス角θの関係を示す．ここで，Q_b1は翼一枚にかかるトルクである．C_Qb1は，どちらの翼形状でもθ = 180°付近で最も高い値を示し，θ = 100°，280°付近で大きく低下している．

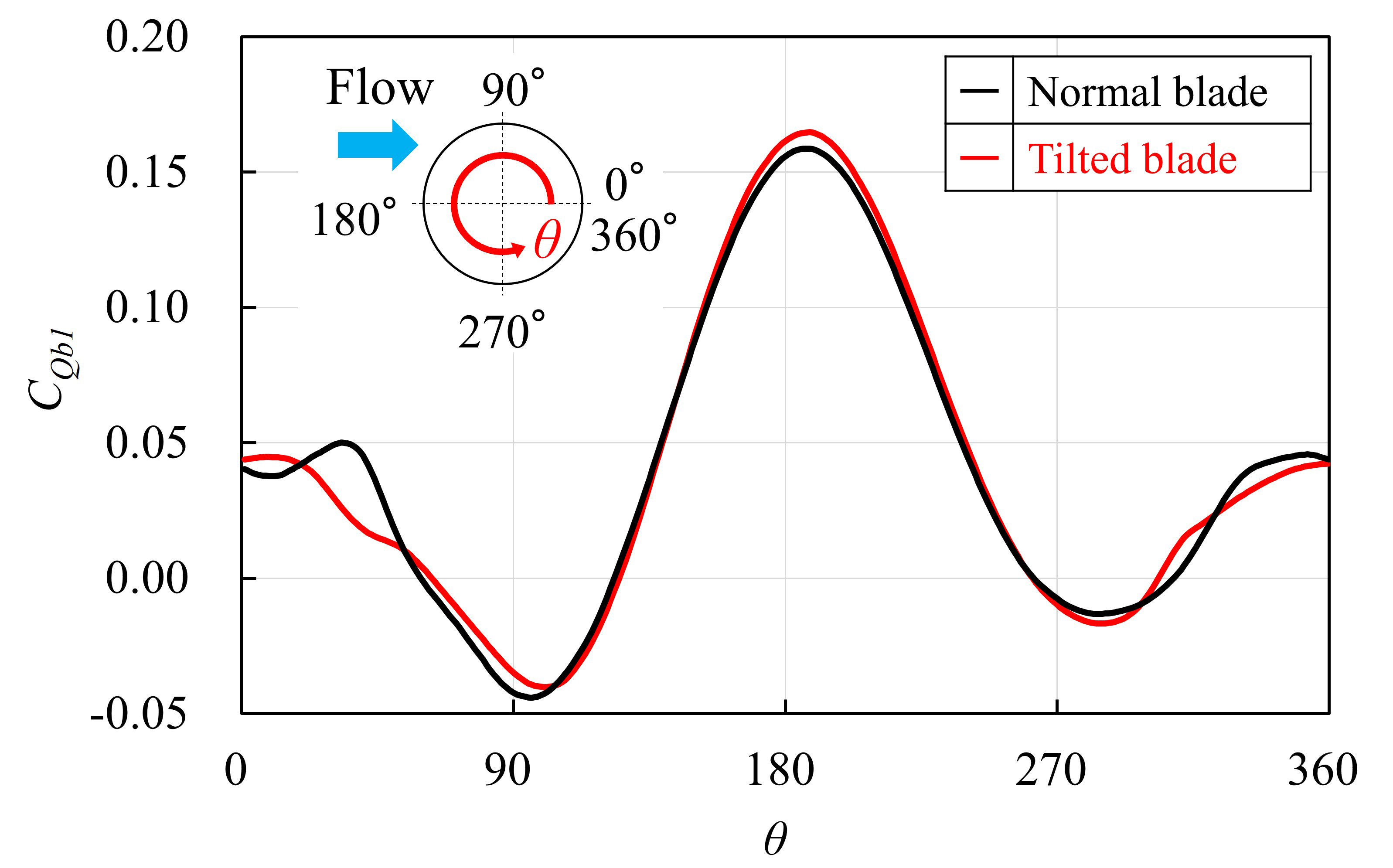
Fig. 9  Torque coefficient of a blade vs. azimuth angle

　図10に，翼下端からの各翼長方向位置におけるトルク係数C_{Qb1_sec} (= 4Q_{b1_sec}/ρAU^_∞2D) の風車二回転分の平均値C_{Qb1_sec} を示す．ここで，Q_{b1_sec} は翼一枚の各翼長位置における翼長方向1セル分の区間にかかるトルクである．どちらの翼形状でも，翼下端から翼長70%位置までは翼の先端に近づくほどC_{Qb1_sec} が増加し，翼長70%位置より先端側では，翼先端に近づくほどC_{Qb1_sec} が低下している．翼長0~90%位置においては，翼形状による大きな差はないが，翼長100%位置においては，通常翼の値が傾斜翼と比較して顕著に大きくなっている．

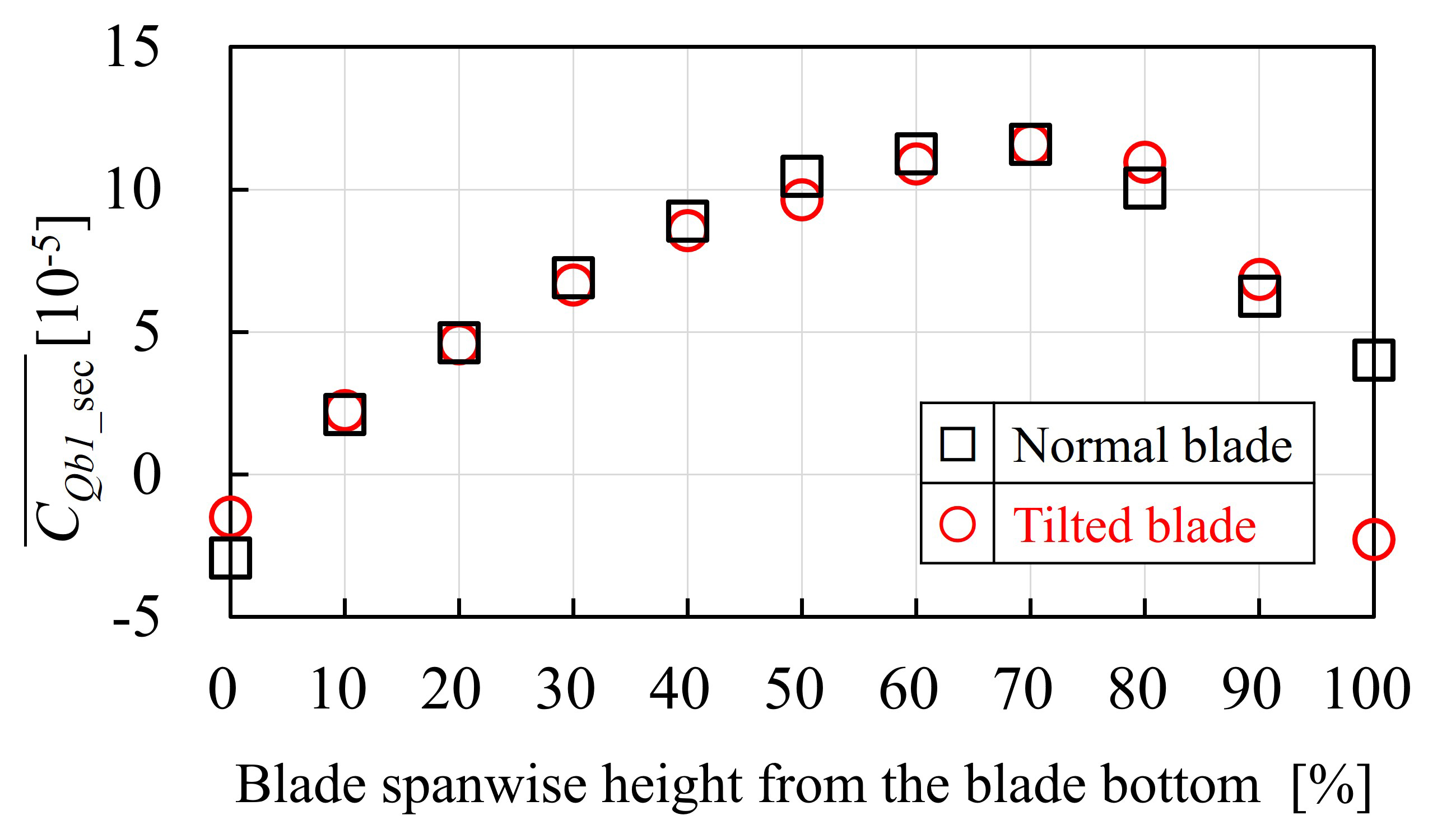
Fig. 10  Mean sectional torque coefficient along a blade

　図11に，各翼長位置のC_{Qb1_sec}とアジマス角θの関係を示す．どちらの翼形状でも翼長0~90%位置においては，C_{Qb1_sec}がθ = 180°付近で最も大きくなり，翼長70%位置でC_{Qb1_sec}の最大値が最も大きくなっている．しかし，翼長100%位置のC_{Qb1_sec}は，θ = 180°付近においてどちらの翼形状でもC_{Qb1_sec}が大きく低下し，θ = 0°付近において通常翼の場合が傾斜翼の場合より顕著に大きくなっている．

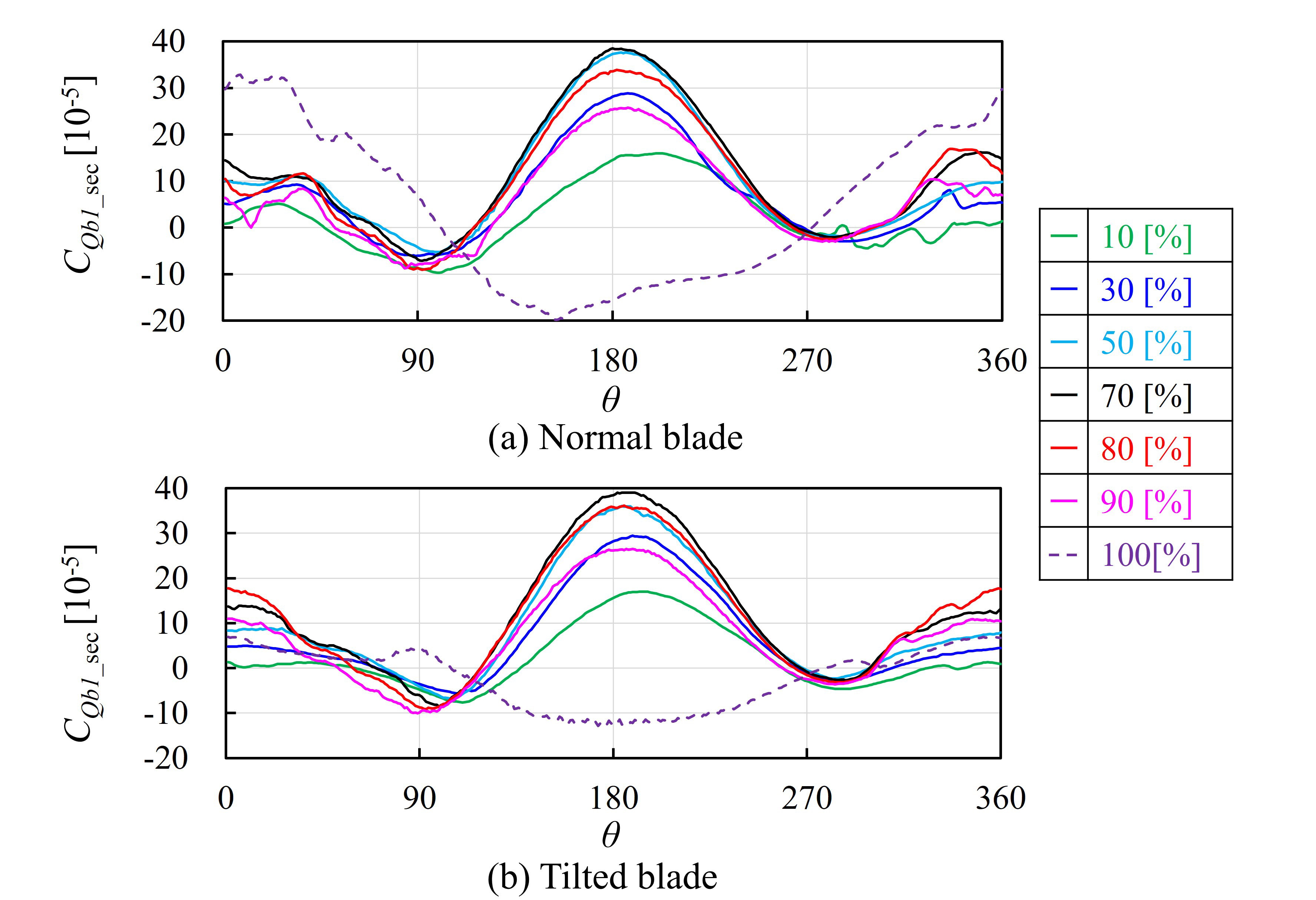
Fig. 11  Sectional torque coefficient of a blade vs. azimuth angle

　図12にθ = 0°における翼長100%位置の圧力係数 ( C_pres = 2(p−p_ref)/ρU_∞² ) の翼型面分布を示す．ここで，pはゲージ圧，prefは流入境界における圧力参照点での圧力である．通常翼の翼前縁付近の正圧の大きさが，傾斜翼と比較して顕著に小さくなっている．これにより，通常翼の翼長100%位置において，θ = 0°でC_{Qb1_sec}が顕著に大きくなったと考えられる．

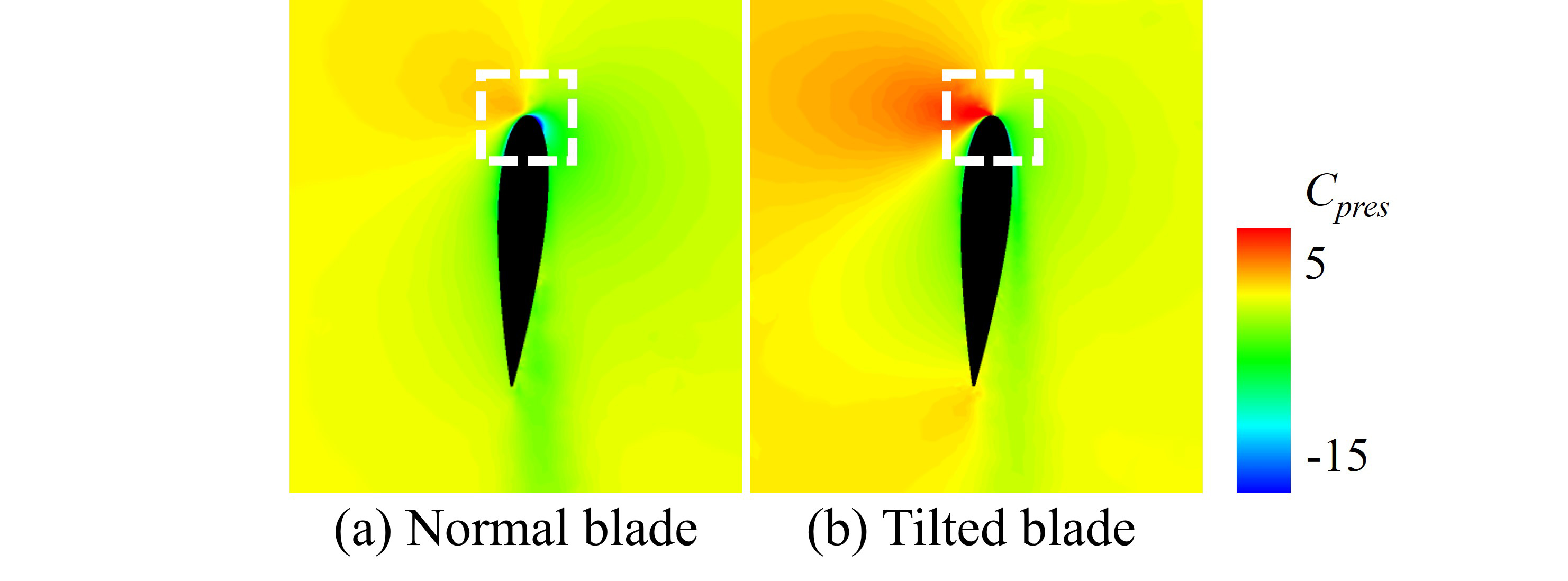
Fig. 12  Distribution of the pressure coefficient on the plane that intersects the blade top as a NACA0018 airfoil at θ = 0°

　図13にθ = 0°かつ翼長100%位置の翼弦25%位置高さにおいて，翼前縁付近（図12白枠）を通過する流線を-y方向から見た図を示す．通常翼では，翼面に沿って上昇する流れが傾斜翼に比べて少ない．この上昇流は翼面に接近するにしたがって流速が減衰し，運動エネルギーが圧力エネルギーに変換されるが，この流れが少ない通常翼では翼前縁付近の圧力が低くなったと考えられる．

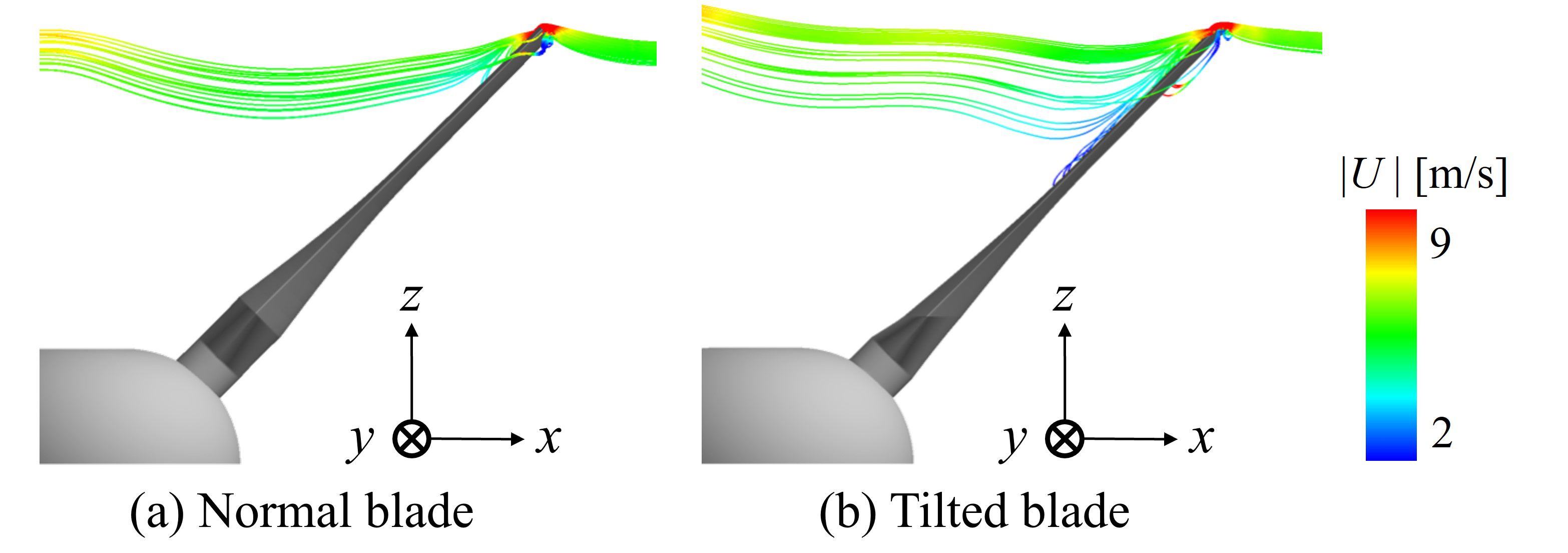
Fig. 13　 Side view of streamlines passing through the vicinity of the leading edge of the blade at top of the blade at θ = 0°

7.　結言

1. 最大出力係数は通常翼より傾斜翼の方が高く，コーニング角50°で最も高くなった．
2. 最適周速比は，傾斜翼より通常翼の方が低く，コーニング角の増加に伴い低下した．
3. 翼一枚あたりのトルク係数は，どちらの翼形状も最風上のアジマス角で最大となり，翼下端から翼長70%位置で最大となった．
4. 最風下付近のアジマス角において，翼先端の翼長方向微小区間のトルクは，通常翼が傾斜翼と比較して顕著に高かった．これは翼面に沿う上昇流が少なく，翼前縁付近の正圧が抑制されたことが原因と考えられる．

謝辞

　本研究における数値計算は，九州大学情報基盤センターのスーパーコンピュータシステムITOおよび京都大学情報環境機構のスーパーコンピュータシステムを利用して実施した．ここに記して謝意を表する．

文献

(1)	D. Todd Griffith et al., Journal of Physics: Conference Series 753, 102003, 2016.
(2)	M.Rahman et al., International journal of green energy, vol.19, No.3, pp.279-299, 2022.