流れ　2016年11月号　目次

―　特集テーマ：2016年度年次大会　― 巻頭言 （藤井，横山，渡辺） 市場にデビューする相反転方式ターボ機械 金元敏明（佐賀大学） 非平衡格子乱流場の特性とスカラー輸送機構 酒井康彦，長田孝二, 伊藤靖仁, 渡邉智昭, 岩野耕始（名古屋大学） ワークショップ：複雑流体の新展開 山本剛宏（大阪電気通信大学），鳴海敬倫（新潟大学），蝶野成臣（高知工科大学） 複雑流体としての生物系粒子分散系 山本剛宏（大阪電気通信大学） 非アファイン性を考慮した高分子添加溶液におけるエネルギー伝達と抵抗低減 －働く高分子と働かない高分子－ 堀内潔（東京工業大学） EFDワークショップ：光学的流体計測手法 渕脇正樹（九州工業大学），飯尾昭一郎（信州大学），稲澤歩（首都大学東京），菊地聡（岐阜大学） 多レンズ多方向光学系の設計および瞬間CT法による非定常流体現象の三次元計測と３Dプリンティング 石野洋二郎（名古屋工業大学） 非定常熱流動場における壁近傍の速度-熱伝達の光学的同時計測について 山田俊輔（防衛大学校），中村元（防衛大学校） 　｜　リンク一覧にもどる　｜

 

非アファイン性を考慮した高分子添加溶液におけるエネルギー伝達と抵抗低減 －働く高分子と働かない高分子－

堀内 潔 東京工業大学

1.　緒　　　言

　 2016年9月11日から14日まで九州大学伊都キャンパスで開催された日本機械学会2016年度年次大会において，山本剛宏先生（大阪電気通信大学）,鳴海敬倫先生（新潟大学）,蝶野成臣先生（高知工科大学）による企画ワークショップ「複雑流体の新展開」で，「非アファイン性を考慮した高分子添加溶液におけるエネルギー伝達と抵抗低減」と題して講演させて頂きました．本ワークショップを企画された先生方をはじめ，この度執筆の機会を与えてくださった日本機械学会流体工学部門の皆様に御礼を申し上げるとともに，以下に筆者の講演内容について紹介させていただきます．

　 Newton 性流体に希薄高分子を添加することにより抵抗低減が起きるというToms 効果⁽¹⁾ は流体の輸送技術やビル空調，地域冷房などの冷媒輸送動力低減技術，省エネルギー化に貢献をしているが，詳細な機構は明らかにされていない．従来，この抵抗低減機構には2 つの仮説が提唱されている．1 つはLumley ⁽²⁾ による，コイル状になった高分子が大きな歪みが起きている領域で伸長され，伸長粘度の増加により抵抗低減が起きるという仮説である．一方，de Gennes  ⁽³⁾ は，高分子が伸長することで弾性エネルギーが蓄積されて張力が発生し，乱流の小スケールへのエネルギーカスケードが抑制されるという仮説を立てた．de Gennes  ⁽³⁾ は，同時に，伸長の大きな高分子は剛性を有して流体の局所的な変形に対する非追随性を示すという仮説を提唱した．実際，高分子応力の構成方程式を用いた解析では，非追随性を考慮した場合，追随性を仮定した場合に比べて顕著な抵抗低減が生じる事がHoriuti et al. ⁽⁴⁾ によって明らかにされた．また，Valente et al. ⁽⁵⁾ は追随性の高分子においてWeissenberg 数が大きな場合，高波数帯域で，溶媒の運動エネルギーから弾性エネルギーへの伝達が顕著に減少して散逸が増大するという結果が報告されたが，この乱流場はelasto-inertial turbulence (EIT) と呼ばれる．本研究では，EIT におけるエネルギー伝達機構を解明する事を目的とし，BDS-DNS法 ^{(6) (7)}による多重スケール解析を行った．

　 本研究ではmacroscopicなスケールの溶媒の運動をNavier-Stokes方程式の直接数値積分 (Direct Numerical Simulation，DNS) で解析し，mesoscopicなスケールでは，高分子鎖をdumbbellモデルで近似してその運動をLagrange 的に直接追跡して溶媒との相互作用をtwo-way couplingで取り入れる計算により，非追随性高分子における顕著な抵抗低減の機構を検証する．

 

2.　Dumbbellの運動方程式

　本研究では，有限伸長を有する2 つのbeads を非線形バネで繋いだdumbbellモデル(Finitely extensible nonlinear (FENE) elastic dumbbell) により高分子鎖を近似する⁽⁶⁾．この高分子鎖の運動と作用する応力をLagrange 的に追跡するが，dumbbellのbeadsを結ぶconnector vector の支配方程式は式 (1) となる．

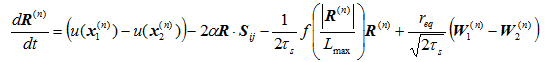(1)

ここに，αは非追随性を表すパラメーター， S=S_ij はstrain rate tensor,  f は FENE 関数，Wは Brownian なノイズを示す. α = 0.0とα = 1.0で各々非追随性が最小，最大となる．式 (1) の右辺第1項をTaylor展開すると，α = 0.0とα = 1.0 の場合，主要部は，各々式 (2)，式 (3) となる，

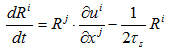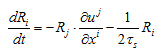 (2)       (3)  

式 (2) ，式 (3) は，各々 upper-convective derivative，lower-convective derivativeで表され，その解は各々反変型，共変型のベクトルとなる．以下，前者を反変型 (contravariant) 高分子，後者を共変型 (covariant) 高分子と呼ぶ．

　 Dumbbell が溶媒に及ぼす高分子応力 τ_ij は式 (4)から算出し，この応力による力をNavier-Stoke 方程式に付加する．

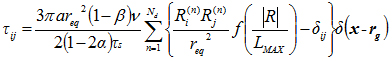(4)

Dummbellのconnector vector の方程式を用いて高分子応力の構成方程式を導出すると，式 (5) のJohnson-Segalmann方程式 ⁽²⁾ となる．

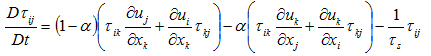(5)

この構成方程式の近似解を求めると式 (6) となる．

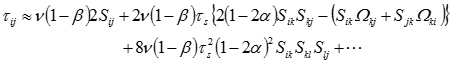 (6)

この近似解を用いて，高分子の弾性エネルギーの生成項P_eを導出すると式 (7)となる．

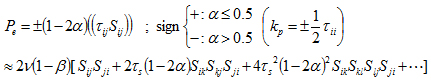(7)

一方，溶媒の散逸率 ε を表すS_ijS_ji 項の支配方程式は式 (8)となる．

(8)　　

3節に示すBDS-DNS計算のデータから，dumbbellの伸長が大きい場合，式 (6)中のS_ikS_kj 項の非対角成分，即ちせん断応力が支配的となる事が示された．したがって，伸長が大きい場合，弾性エネルギーの生成項と散逸率の生成項 P_ε の主要項は，反変型高分子では，

　(9)　　

共変型高分子では，
　(10)

となる．Strain skewness 項 -SikSkjSji では正値が支配的である事を考慮すると，反変型高分子では弾性エネルギーが溶媒の運動エネルギーに変換されて散逸の生成に寄与するのにたいし，共変型高分子では弾性エネルギーと散逸の双方の生成に寄与するものと予測される．

 

3.　 BDS-DNSの計算結果

　流れ場は強制一様等方乱流⁽⁷⁾ とし，計算領域は全方向に2π，周期境界条件を適用した．格子点数は128³，粘性係数はν = 1/30 とした．時間積分には3 次精度Runge-Kutta 法を用い，Δt = 0.001 とした．空間の離散化にはスペクトル法を用い，aliasing 誤差は3/2 則により除去した．Dumbbell の最大長はNewton 性流体のKolmogorov長ηとしL_max = 0.1，dumbbellの平衡長はr_eq = L_max/50 とした．緩和時間τs はKolmogorov時間スケールτηに対して，Wi = τ_s /τ_η で定義されるワイゼンベルグ数をWi = 10.0 とした．

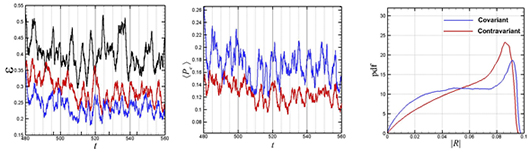
Fig.1 Temporal variations in ε.	Fig.2 Temporal variations in Pe.	Fig.3 p.d.f. of the dumbbell length

    図1 と図2 に溶媒の散逸率と高分子の弾性エネルギー生成項P_εの時間発展を示す．赤線は反変型，青線は共変型，黒線はNewtonianを示す．散逸率ε は抵抗低減の指標であり，小さな値をとるほど顕著な抵抗低減を得られていることを意味する．抵抗低減の大きさは共変型，反変型，Newtonian の順になっている事から，共変型において顕著な抵抗低減が起きていることが判る．図2 よりP_eは共変型高分子の方が大きな値を取っていることが見て取れる．図3に，高分子の長さの確率密度関数(p.d.f.) を示す．最大伸張をとる確率は，共変型高分子が反変型高分子に比べて大きい事から，共変型高分子においてより大きな粘弾性効果が起きているものと考えられる．

 

4.　Dumbbell の配向とエネルギー伝達

　本節では，高分子の配向を検証するが，ここでは，2種類の固有ベクトルを基底とした座標系を設定する．一つは，strain rate tensorS_ij の固有ベクトルであり，e_s, e₊, e_-,と記述する．ここに，3固有ベクトル中で渦度ベクトルに最も平行な固有ベクトルをe_s，残りの2ベクトル中で対応する固有値が大きなベクトルをe₊，残りをe_-,とする．もう一つは [A_ij]≡ (S_ikΩ_kj+S_jkΩ_ki) 項の固有ベクトル，a_s, a₊, a_-に依る基底である（Ω_ij は渦度テンソル)． BDS-DNSデータの解析から，dumbbellの伸長が大きな場合，最大頻度で抽出される上記固有ベクトルとdumbbellの配向は，反変型高分子ではR//e_s，共変型高分子ではR//e_-となる事が示された（図は省略）

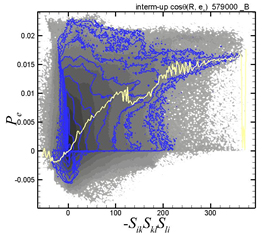
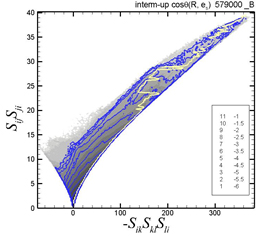
　 図4 と図5 に，反変型高分子における -S_ikS_kjS_ji 項と各々P_e，S_ijS_ji.項とのjoint p.d.f. を示す．但し，ここでは，S_ij項等については，DNSの格子点での値をdumbbellの重心での値に補間して各項を算出している．青色の等高線は，|cosθ(R, e_s)| ～ 1 の条件付きに抽出されたjoint p.d.f.を示し，黄色の曲線は確率が最大となる点を連ねた分布を示す．Rと e_s が平行に近い場合，-S_ikS_kjS_ji 項の増加と共にP_e項は減少するのに対して，S_ijS_ji項の生成は増加する事が見て取れる．したがって，弾性エネルギーの生成は減少するのに対し，溶媒の散逸へのエネルギー伝達が増大する事を示し，3節での式 (9)による解析的な予測と整合する．この結果は，Valente et al. ⁽⁵⁾によるFourier空間におけるEITの実空間における記述を与える．

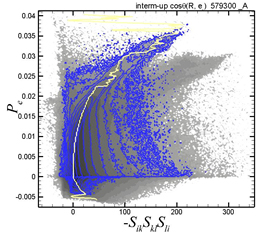
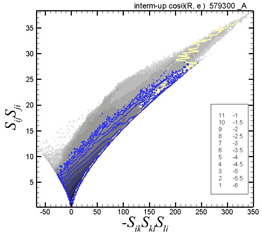
　 図6 と図7 に，共変型高分子における -S_ikS_kjS_ji 項と各々P_e，S_ijS_ji項とのjoint p.d.f. を示す．青色の等高線は，|cosθ(R, e_-)| ～ 1 の条件付きに抽出されたjoint p.d.f.を示し，黄色の曲線は確率が最大となる点を連ねた分布を示す．Rと e_- が平行に近い場合，-S_ikS_kjS_ji 項の増加と共にP_e項の値は増大するのに対して，S_ijS_ji項の生成は，小さな値の-S_ikS_kjS_ji 項で飽和に達する事が見て取れる．したがって，弾性エネルギーの生成は増加するのに対し，溶媒の散逸へのエネルギー伝達は減少する．3節の式 (10)からは両方向へのエネルギー伝達が考えられたが，実際の高分子では，弾性エネルギー生成への伝達が，溶媒の散逸への伝達に卓越する事が示された．このため，共変型高分子では顕著な抵抗低減が起きるものと考えられる．

Fig.4 Joint p.d.f. between -SikSkjSji and Pe . Blue contours: conditioned on R//es	Fig.5 Joint p.d.f. between -SikSkjSji and SijSji. Blue contours: conditioned on R//es
Fig.6 Joint p.d.f. between -SikSkjSji and Pe . Blue contours: conditioned on R//e-	Fig.7 Joint p.d.f. between -SikSkjSji and SijSji. Blue contours: conditioned on R//e-

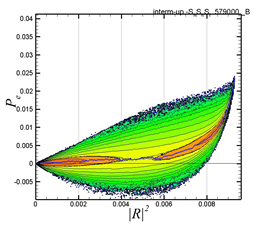
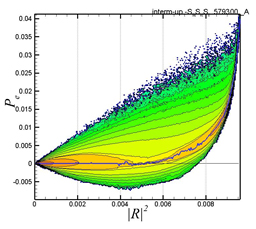
　図8 と図9 に，各々，反変型高分子と共変型高分子における |R|² とP_e項のjoint p.d.f. を示す．黒色の太い曲線は確率が最大となる点を連ねた分布を示す．Dumbbellの伸長が中間値の領域では，反変性では単調にP_e項の値が増加しているのにたいして，共変性ではP_e項の値は零値付近に集中している．一方，dumbbellの伸長が最大値近辺では，共変性ではP_e項の値が顕著に増加するのにたいして，反変性では増加は小さい．したがって，dumbbellの伸長が中間値の領域では，反変性高分子が高分子エネルギーの生成において機能するのにたいして，最大値近辺の領域では，共変性高分子が機能しており，反変性と共変性高分子の機能には，棲み分けが存在する事が分かる．この結果は，働くアリと働かないアリの機能の棲み分け⁽⁹⁾に類似しており，自然界における系全体の普遍的な維持機構である可能性が考えられる．

Fig.8 Joint p.d.f. between |R|2 and Pe .      obtained in the case with α=0.0-	Fig.9 Joint p.d.f. between |R|2 and Pe obtained in the case with α=1.0- -

 

7.　結　　　語

　本研究では，高Weissenberg 数における，高分子添加溶液の抵抗低減機構の解明をBDS－DNS 法を用いて行い，以下の結論を得た．
・反変型高分子は大きく伸長した時，伸長過程で貯蔵した弾性エネルギーを保持できず，溶媒の運動エネルギーに伝達するため，散逸の生成が増大することを示した．
・共変型高分子は，最大に伸長した時，伸長過程で貯蔵した弾性エネルギーを保持するため，顕著な抵抗低減が得られることを明らかにした．
・本研究の結果は，伸長の大きな高分子が剛性を有するというde Genne の仮説に対する支持を与える．図3から，反変型高分子では，大きな長さを持つdumbbell数が単調に増加する事が見て取れるが，これは，反変型高分子はflexibleなためcoilした状態から容易に伸長されるが，大きく伸長されると今度は容易に収縮するためと考えられ，反変型高分子は必ずしも有効な抵抗低減の添加媒体ではない可能性がある．一方，共変型高分子ではp.d.f. が2つの極大値を持つ事が見て取れる．これは，共変型高分子は剛性を有するため，coilした状態からの伸長を拒絶するが，いったん伸長した場合は収縮しにくくなるためと考えられる．したがって，抵抗低減に最も有効な高分子は，伸長が中間値の場合は反変性を示し，伸長が最大長に近い場合は共変性として振舞う高分子と考えられる．実際の高分子における挙動の検証が今後の課題となる．

 

文献

(1)	Toms, B. A., Some observations on the flow of linear polymer solutions through straight tubes an . large Reynolds numbers, In Proc. 1st Intl Congr. Rheol.,, 1 (1949), 135–141.
(2)	Lumley, J. L., Drag reduction by additives, Annual. Review of Fluid Mechanics., 1 (1969), 367-384
(3)	Taybor, M. and Gennes, P. G. D., A Cascade Theory of Drag Reduction, Europhys. Lett., 2(7) (1986), 519–522.
(4)	K. Horiuti, K. Matsumoto, and K. Fujiwara., Remarkable drag reduction in non-affine viscoelastic turbulent flows, Phys. of Fluids 25, 015106 (2013).
(5)	Valente P. C., da Silva, C.B. and Pinho, F.T., The effect of viscoeleasticity on the turbulent kinetic energy cascade, J. Fluid Mech, 760 (2014).
(6)	Watanabe, T. and Gotoh, T., Hybrid Eulerian- Lagragian simulations for polymer-turbulence interactions, J. Fluid Mech, 717 (2013), 535–575.
(7)	竹生, 堀内, 増田, BDS－DNS 法による高分子添加液における抵抗低減機構の解明, 第27 回数値流体力学シンポジウム, C10 －-3 (2013).
(8)	Johnson, M. W. and Segalman, D., A model for viscoelastic fluid behavior which allows nonaffine deformation., J. Non-Newt. Fluid Mech., 2 (1977), 255.
(9)	長谷川英祐，『働かないアリに意義がある』メディアファクトリー (2010).