流れ 2017年2月号 目次
― 特集テーマ:流体工学部門講演会 ―
| リンク一覧にもどる | |
21世紀の乱流研究
柳瀬 眞一郎
|
1. スタンフォード会議 1980-1981年
1980年と1981年の2回,どちらも9月に,スタンフォード大学で Klineが中心となって,別名クラインのオリンピックと呼ばれた乱流モデルの検討会が開かれた.1980年の会合の報告は,ASME の論文(Kline et al., 1980)として発表された.モデルの本格的な検討はここで行われたようで,1981年の会合はその成果報告会で例えばオリンピックの表彰式のようなものであったらしい.著者は1981年のみに参加した.
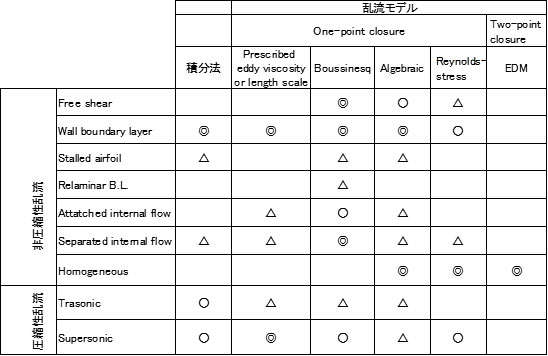
Table 1に提出された計算リストを示すが,マークは提出計算結果数の多少を示しているだけである(◎,○,△の順で多い).最終日に発表された結論はどの乱流モデルもとりわけ優れているとは言い難いという結果で,あたかも表彰式のないオリンピックのようなものであった.後日,参加者には表1のような結果が送られてきたが,おそらくASMEには報告論文はなかったと思われる.なお,著者は1981年の会の様子を日本物理学会誌で報告した(柳瀬,1982).この会に参加した日本人の数は極めて少なく,5名と発表されていて,計算結果を提出したのは三菱重工業の永松哲郎氏ただ一人であった.それ以外に,東京理科大学の本阿弥真治教授は会の運営に尽力されていた.この会議後,本格的にスーパーコンピュータが稼働を開始し,LESが実用期を迎えることとなる.
Table 1 Submitted turbulence calculations to Kline’s Olympic.
2. 乱流計算法の進歩(大衆化)
20世紀の最後の20年間はスーパーコンピュータの時代であった.それに対して21世紀は超並列コンピュータとPCの時代と呼んでもいいかもしれない.特に近年のPCの低価格化と大容量メモリの進歩は目覚ましく,例えば著者が最近調べた例では,Core/i7のプロセッサに32GBのメモリを搭載したPCが12万円強で手に入る.5123 の倍精度実数配列は約1GBであるため,32GBはこの程度の大きさの3次元計算が可能なメモリ量であることが分かる.したがって,安価なPCで巨大計算が可能な時代となったのは事実である.さらにフリーで優れた性能を持つCFDソフトが普及してきたため,乱流計算の大衆化とも言える時代に入った.複雑な流れを LESを用いて計算し,実験結果と比較的良い一致を示した例を図1に挙げる(河内等,2015).これは閉領域内の回転円盤下部に発生した秩序渦構造を Q値を用いて示したものである.

Fig.1 Q-value representation of the coherent vortices beneath the rotating disk.
3. マイクロバブル乱流の研究
今日多くの機能性流体と呼ばれるものが人工的に作られ研究されている.しかし,実用的に有用であることが示されたものはそれほど多くなく,流体はやはり空気と水であるという意見も依然有力である.その中で,直径数10µmの気泡を多数含むマイクロバブル流は現実に多くの分野で利用が進んでいる(柳瀬,松浦,2015).マイクロバブルについては,西日本乱流研究会で長らく活躍された大成博文教授の業績に注目しないわけにはいかない.
その中でも抵抗低減は重要な工学的応用であり,船舶への適用に関して,本報告の第1節で紹介した永松氏が船舶の抵抗低減に関する論文を発表されていることは,著者にとっては大変興味深い.この問題に関しては実験的研究は大変困難で,抵抗低減が実現できるような実験環境を構成することもそれほど容易ではない.管内流における抵抗低減は実際には乱流遷移をより高いレイノルズ数へ移動させるという形で生じているが,この問題に関する原理的な解決に少しでも近づくことが望まれている.本問題を特に困難にしている原因は,現在の乱流研究において多分最も有力な手段である数値計算法が,多数のマイクロスケール気泡の運動を正確に取り扱えないために決定的な結果を与えることができないという点である.この問題を克服し,マイクロバブル流の遷移を解明することは,マイクロバブルを含まない通常流体の遷移の根本的な解決にもつながるのではないかとひそかに期待している.なお,マイクロバブル流の先にはナノバブル流があり,ここはまだ魑魅魍魎の世界である.
4. コルモゴロフの法則の再考
慣性小領域とはエネルギースペクトルE(k) ∝ k-5/3 となる波数領域で,Batchelorの古典的な書物“乱流理論”(Batchelor, 1960)のp.115に,「慣性小領域が存在するためにはReynolds数は平衡領域の存在のために必要なものの自乗の程度でなければならず,これは明らかに実験室の風洞では実現されそうにはない」とある.このコメントは“乱流理論”の占める圧倒的な地位故に,多くの乱流研究者を,あるいは著者だけかもしれないが,呪縛してきた.図2は一様等方乱流のエネルギースペクトルE (k) とエンストロフィースペクトルk2E (k) の典型的な形状を,対数ではなく線形スケールで示したものであり,比例定数は省いてある.
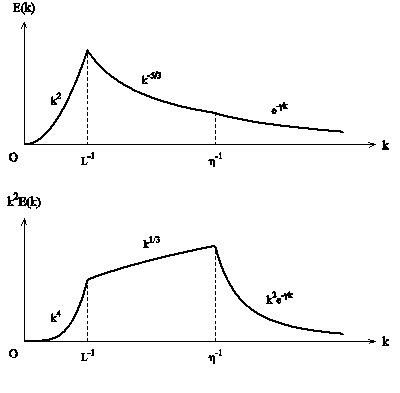
Fig.2 Energy spectrum and enstrophy spectrum
しかし,近年多くの実験室風洞で,あまり広い波数領域ではないが慣性小領域が頻繁に観測されている.さらに,明らかに完全発達乱流と言えない間欠的な乱流でも慣性小領域が観測されていて,現在,慣性小領域の成立条件,遍在性に関して根本的な見直しが必要なのではないかと考えられる.本問題に関して,最近のVassilicosの論文が参考になる(Vassilicos, 2015).
5. これからの研究方向について
乱流は確率的な現象であることは周知の事実であり,有名なMoninとYaglomの大著の題名は統計流体力学である(Monin and Yaglom, 1971).しかし,確率論的なアプローチが直接的に役立った例はそれほど多くないと思われる.その原因としては,ナビエ・ストークス方程式があまりに複雑で,確率論の簡単な定式化を受け付けないからであると思われる.一方,筆者の実験室の風洞で得られたデータを見れば,乱流の速度場が典型的な確率分布を持っていることが示されている(柳瀬,2015).
今後,乱流現象の確率的・統計的な取り扱いが急速に進展すると思われるが,その原動力となると考えられるのは近年劇的に進化したPIV等の測定技術とその処理速度の高速化・大容量化である.これに確率論の3次元複雑場への拡張の発達が伴うならば,乱流の確率的な解析が大きく進歩することが期待される.
以上,個人的な視点から21世紀乱流研究の展望の一端を紹介したが,これまで想像もしなかったような分野での研究の大爆発が21世紀に発生することを期待してやまない.
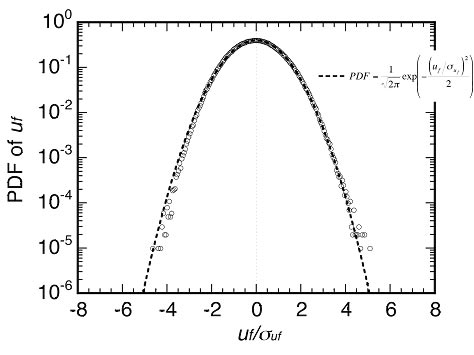
Fig.3 (a) PDF of the velocity field.
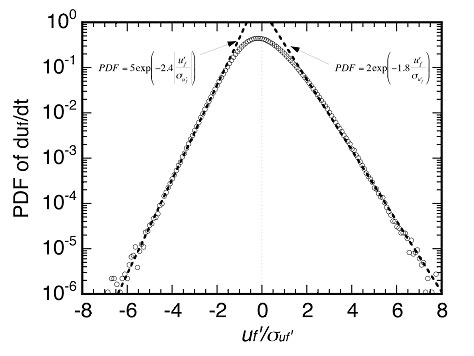
Fig.3 (b) PDF of the time derivative of the velocity field.
文 献


