流れ 2017年2月号 目次
― 特集テーマ:流体工学部門講演会 ―
| リンク一覧にもどる | |
液晶流を利用した無定形アクチュエータ
松田琳子 (高知工科大学)
|
1. 緒言
山口大学宇部キャンパスで開催された第94期機械学会流体工学部門講演会において,若手優秀講演フェロー賞を頂きました.本稿では部門講演会での発表内容である,液晶流を利用した無定形アクチュエータについて紹介させていただきます.
近年,液晶の流動を利用した液晶平板アクチュエータや液晶モータの開発が行われている(1~4).これらのアクチュエータでは,棒状の液晶分子が電場方向へと回転する際に生じる流動を利用して,平板あるいは円筒を駆動させる.一方,駆動源である液晶は液体状であり,固有の形状を持たないという性質がある.この性質を応用し,マイクロサイズの液晶滴に電場を印加することで,アメーバのように自身の形状を自在に周囲環境に適合させながら駆動することができる液晶無定形アクチュエータの開発が現在行われている(5).液晶無定形アクチュエータが実現すれば,毛細血管のような軟らかい外壁や網目状の複雑な構造をもつ微小経路を介して薬を運ぶことができ,現在の医療技術での治療領域に対してより微小な領域の治療が可能となると考えられる.
本研究では,液晶流を利用した無定形アクチュエータの実現を目指し,基板上の液晶滴に横電場を与えた場合の液晶滴重心変位の印加電圧値依存性および液晶滴直径依存性を明らかにする.さらに,一様な縦電場を用いた液晶滴の駆動を試みる.
2. 横電場印加実験
2.1. 実験装置および方法
図1に実験装置の概略図を示す.一対の金電極(電極間隔15µm,電極幅5μm)が施されたガラス基板上に液晶滴を設置する.このとき,図1に示した右側電極の左端に液晶滴の右端が接する状態にする.基板表面には垂直配向膜が成膜されており,基板面上における液晶分子の長軸は基板面に対して垂直となる.基板上の電極間に電位差を発生させることで液晶滴に横電場を1秒間印加する.このときの液晶滴の挙動を水平方向から撮影する.実験パラメータは印加電圧値V,液晶滴直径φであり,実験回数はそれぞれ10回とする.
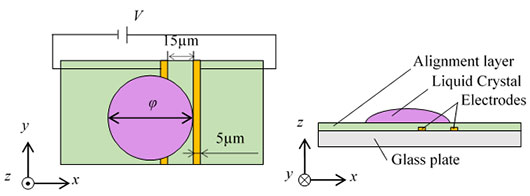
Fig. 1 Schematics of an experimental setup
2.2. 実験結果および考察
図2に基板上に滴下された液晶滴に電場を印加した際の,電場印加開始時刻t=0sから電場印加終了時刻t=1sまでの液晶滴の駆動の様子を示す.印加電圧値V=90Vおよび液晶滴直径φ=50µmである.液晶滴は電場印加直後より形状変化をともなって駆動する.また,液晶滴はt=0.5sでほぼ駆動を終える.図3に液晶滴直径φ=50µmの場合の液晶滴の重心変位Lと印加電圧値Vの関係を示す.図中のエラーバーは標準偏差である.V≲100VにおいてVの増加にともなってLは増加し,V≳100VでLはほぼ一定の値(L≈17.5µm)を示す.液晶滴の初期重心位置から電極間隔中心までの距離は17.5µmであり,Lは17.5µm付近でほぼ一定値となることから,液晶滴の初期重心位置から電極間隔中心までの距離が,液晶滴重心位置の最大変位量であると考えられる.図4に印加電圧値V=90Vの場合の液晶滴の重心変位Lと液晶滴直径φの関係を示す.φ≲80µmにおいて,Lはφの増加にともなって増加し,φ=80µmで最大値を示す.また,φ≳80µm ではLは減少する傾向を示す.φの増加は,上述の液晶滴重心位置の最大変位量の増加と駆動体である液晶の質量の増加をもたらす.φ≲80µmでは液晶滴重心位置の最大変位量の増加にともなって変位量が増加するが,φ≳80µmでは液晶の質量の増加により変位量が減少したと考えられる.
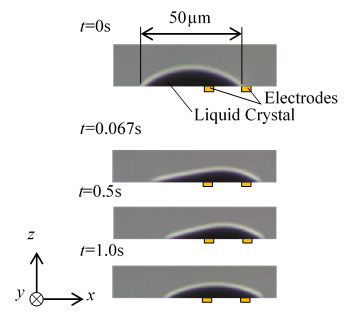
Fig. 2 Motion of liquid crystalline droplet under transverse electric field
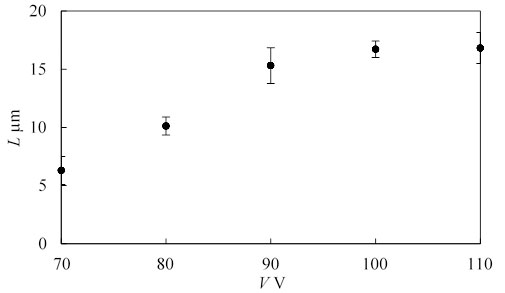
Fig. 3 Dependence of actuator displacement on imposed voltage
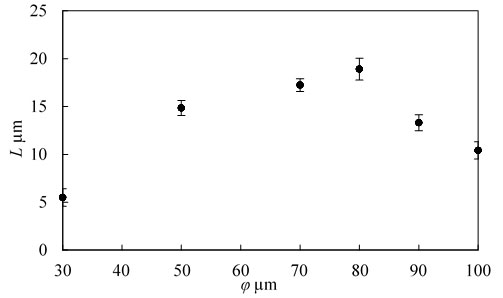
Fig. 4 Dependence of actuator displacement on droplet size
3.縦電場印加実験
3.1. 実験装置および方法
前章の実験では,基板面に対して平行な横電場を用いて液晶滴の駆動を試みている.従って,横電場の実現のために複雑にパターニングされた電極を必要とする.ここでは,基板面に対して鉛直な一様電場を用いて液晶滴の駆動を試みる.基板面に対して鉛直方向に電場を発生させるためには,液晶滴の上下に電極を設置する必要がある.図5に実験装置の概略図を示す.直径100μmの液晶滴を,二枚のガラス基板を用いて作成したセル内に設置する.なお,セルの上下基板内側には,ITO電極が一様に成膜され,さらに液晶分子が基板面に対して水平に配向するように水平配向処理が施されている.セル内の液晶滴に上下の電極を介して一様なz方向の電場を印加する.このときの液晶滴の挙動をz方向から撮影する.
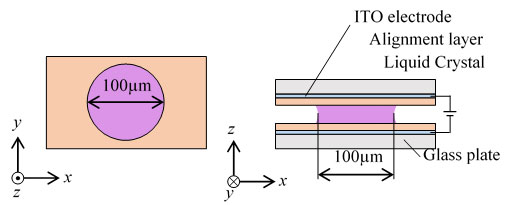
Fig. 5 Schematics of an experimental setup
3.2. 実験結果および考察
図6にパルス電圧印加開始時刻t=0sから電圧印加終了時刻t=4sまでの液晶滴の挙動の様子を示す.印加電圧値90V,上下基板間隔6µmである.液晶滴の初期重心位置を白色×印,各時刻tにおける重心位置を黒色×印で示す.図6より電圧印加によって,液晶滴がx軸負の向きに駆動することに成功している.また,前述した横電場では液晶滴は形状変化をともなって駆動することに対し,縦電場では液晶滴はほぼ形状変化することなく駆動する.

Fig6 Motion of liquid crystalline droplet under vertical electric field
4. 結言
液晶流を利用した無定形アクチュエータの実現を目指し,横電場および縦電場を与えた際の液晶滴の駆動について以下のことを明らかにした.
- 液晶滴直径φ=50µmの液晶滴に横電場を印加した場合,印加電圧値Vを上昇させると液晶滴の重心変位Lは増加し,V≳100VでLは一定の値(L≈17.5µm)になる.
- 液晶滴にV=90Vの横電場を印加した場合,φを増加させるとLは増加し,φ≈80µmでLは最大となる.
- 一様な縦電場を印加した場合の液晶滴の駆動にも成功した.
以上より,横電場を液晶滴に印加した際の液晶滴重心変位の印加電圧値依存性および液晶滴直径依存性といった駆動特性を明らかにしました.また,縦電場印加における液晶滴の駆動に成功しました.将来的に横電場および縦電場を用いて液晶滴の三次元的な駆動を実現するために,今後さらに研究活動に励んでいきたいと考えています.
謝辞
講演会当日に本発表および討論において大変貴重な意見と質問を頂きました先生方,選考委員会の皆様,ならびにニュースレター執筆の機会をくださった日本機械学会流体工学部門関係者の皆様に心から感謝いたします.
引用文献


