流れ　2020年12月号　目次

―　特集テーマ：2020年度年次大会　― 巻頭言 （本澤，森） 乱流のLarge Eddy Simulation の課題 梶島 岳夫（大阪大学） ターボ機械内部流の非定常性について（現象理解と空力・伝熱設計への展開） 船﨑 健一（岩手大学） 固体高分子形燃料電池におけるガス拡散層内部の蒸発を伴う二相流解析モデルの構築 長山 龍也，境田 悟志，田中 光太郎，金野 満（茨城大学） 粒子追跡法によるナノ空間流速分布計測に向けたナノ粒子挙動の統計力学的解析 田中 美典（慶應義塾大学），花崎 逸雄（東京農工大学），嘉副 裕（慶應義塾大学） 年次大会の備忘録　―ウェブ開催の運営的立場から― 伊藤 靖仁（名古屋大学） 年次大会 流体工学部門OS「流体工学の基礎と応用」開催の経緯 および変遷 （森） 　｜　リンク一覧にもどる　｜

 

乱流のLarge Eddy Simulation の課題

梶島 岳夫 大阪大学

１．背景

　Large-Eddy Simulation (LES)に関する乱流モデルや数値計算法の詳細については，紙面の都合により割愛するので，参考文献も含めて拙著⁽¹⁾⁽²⁾を参照いただきたい．

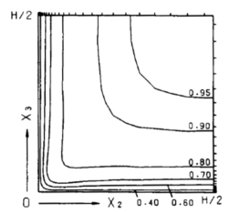
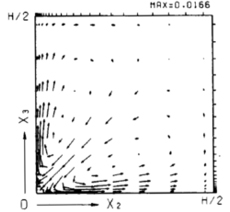
　乱流のLESの基本形であるSmagorinskyモデルの提案は半世紀前で，レイノルズ平均に対する標準的なk-ε二方程式モデルや応力方程式モデルより古く，1980年代のいわゆるスーパーコンピューターの出現前の1963年に遡る．平行平板間流れに対して，壁関数モデルを用いたDeardorff，ノンスリップ条件を用いたSchumannにより，それぞれ1970，1975年に公表されたLESの計算結果は，乱流における基本的な問題の多くは数値シミュレーションによって解決できるのではないかと期待させるに十分なインパクトがあった．筆者にとっては，大学院に進学したときに当時の三宅裕助教授からNikuradseによる矩形断面流路内乱流の速度分布の図面とともにDeardorffの論文を渡され，LESという新しい方法によってPrandtlの第二種二次流れの問題が片付くのではないかと示唆されたことが乱流の数値シミュレーションに関わる端緒となった．博士課程では回り道をして，第二種二次流れに対して満足できる結果⁽³⁾を論文化できたのは学位取得後であった．その過程で，ノンスリップ条件を用いることが本質的であることを知った．壁面上では流速はゼロとなるのに対して壁面に沿って圧力勾配が生じることが駆動力になることは，遠心力やコリオリ力による第一種二次流れと共通している（図1）．この場合の駆動力は，二次流れの原因と指摘されていたレイノルズ応力の副次的な成分とそれに起因する圧力勾配の局所的なずれ
　　
から説明することができた．この解析手法は，のちに様々な場面で重宝した．

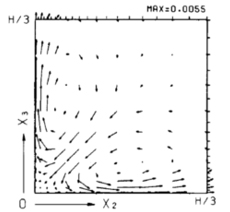(a) 主流速度分布	(b) 断面二次流れ	(c) 二次流れの駆動力 DT
図1　LESにより求められた矩形断面流路内乱流の第二種二次流れ (3)

　ノンスリップ条件の導入は，粘性流体の流れの数値シミュレーションにおけるプログラミングではさほど困難ではないが，高レイノルズ数の乱流においては固体壁近傍で非常に細かい格子分割を必要とするため計算負荷が増大する．LESのSubgrid Scale (SGS)モデルや関連するアイデアは，Smagorinskyの渦粘性モデル（1963年），Leonardによるフィルタリング（1974年），Bardinaらのスケール相似則モデル（1980年），Gernanoらのダイナミック渦粘性モデル（1991年）と，前世紀には概ね10年ごとに大きな進展があった．しかし，今世紀に入ってから，これらに匹敵する本質的な変革は見当たらない．ただし，長年の懸案である固体壁近傍の対処法については，非等方性を考慮したモデル⁽⁴⁾，壁法則モデル⁽⁵⁾により見通しがついてきたと考えている．一方で，空間的に非一様なフィルター操作と微分操作のcommutationの問題など，以前から指摘されているにもかかわらず，有効な打開策が見当たらず，不整合を残した基礎式が用いられる状態が続いている．

２．基礎方程式の再構築

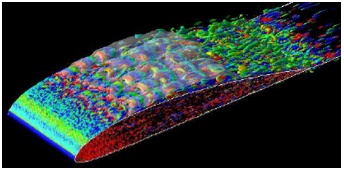
　筆者らは，多相乱流への関心から，固体粒子と乱流の相互作用⁽⁶⁾⁽⁷⁾，熱伝達をともなう固液二相乱流⁽⁸⁾，キャビテーション乱流⁽⁹⁾の解析を行っている．図2に，Clark-Y11.7%翼のキャビテーションによる揚力ブレイクダウン前後のキャビテーション数における瞬時の流れ場（スパン方向渦度で着色されたQ値と半透明の白色で表示されたキャビティ領域）の一例を示す．これらの計算ため，個々の粒子のまわりの流れや温度場も扱う直接計算から，キャビティ体積率を考慮した基礎方程式によるLESまで，対象と目的に応じて現実的な手法を開発している．気液二相流におけるボイド率，固気または固液の二相流における体積率はいずれも平均値である．流れ場の大域的な体積率は明確に定めることができても，二相乱流のLESの変数となる局所的な体積率の定義，これと乱流に対する空間フィルター操作との関係については，必ずしも十分に検討されていない．そのような支配方程式に依存しているのが二相乱流のLESの現状である．

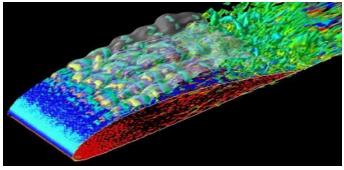(a) σ=0.8	(b) σ=0.6
図2　 Clark-Y11.7%翼まわりのキャビテーション乱流の瞬時の流れ場の例(9)

　固体粒子による乱流変調（乱れの強さの増減）において，粒子径とコルモゴロフスケールの大小関係は重要なパラメーターである．そこで，コルモゴロフスケールの粒子が乱流に及ぼす影響の解明を目的とする数値計算を想定しよう．個々の粒子のまわりの流れも解像するためには，バックグラウンドの乱流を単相で直接計算する場合に比べて1～2桁は格子を細かくしなければならない．しかし，広い計算領域を扱うためには，格子幅はコルモゴロフスケール（この場合は粒子径）より細かくしたくない．また，仮定の多い質点モデルを使わず，格子ごとに含まれる固体表面での相互作用を導入するには，それなりの平均操作が不可欠である^(10)(11)．様々な目的で二相流を計算するための支配方程式の導出にあたっては，例示したコルモゴロフスケール粒子に限定するようなオーダーメイドではなく，幅広いスケールにわたって普遍的な手法が必要である．多相系の乱流については，これを如何なる形式でLESの基礎式として表現すべきかまで立ち返って追究すべきであると考えている．

３．展望

　乱流の数値シミュレーションの分野においても，機械学習の導入は，その是非も含めて不可避的な検討課題であろう．多様な乱流場に対して教師データの質と量を充実させること，乱流応力のrealizabilityやテンソル法則に整合するように学習させることの重要性はすでに指摘されている⁽¹²⁾．さらに，産業応用にあたってはV&V（Verification and Validation）に耐えるための指針をつくらなければならないだろう．LESへの応用についても，重要な因子を選ぶ段階から，モデルを選ぶ，モデルをつくるレベルまで発展するかもしれない．数値計算法と物理モデルの双方を意識した導入法も検討されている⁽¹³⁾．今後は，計算と実験のそれぞれに対して機械学習を導入するだけでなく，保存則に基づく数値計算に対して疎らでノイズの大きいデータを同化させるための機械学習の方法を開発することも有効ではないだろうか．いずれにしても，機械学習と数値計算の意味のある関係づけのためには，確固とした基盤が不可欠であり，LESの場合には前述したようなフィルターをかけた場の基礎方程式の再構築の必要性を重ねて強調しておきたい．

謝辞

　本稿は2020年度年次大会における基調講演論文に加筆したものである．図１の結果を携えて初めて参加した国際会議で出会い，CFDについて語り合ってきた長年の友人である山本悟教授が司会してくださったので，感慨を覚えて古風な図面を引用した次第である．山本教授をはじめ，流体工学部門の関係各位に感謝申し上げます．

文献

(1)	梶島岳夫，“乱流の数値シミュレーション 改訂版”，養賢堂 (2014).
(2)	Kajishima, T. and Taira, K., “Computational Fluid Dynamics --- Incompressible Turbulent Flows”, Springer (2017).
(3)	梶島岳夫, 三宅裕, 西本俊幸, “正方形断面流路内の乱流のLES”, 日本機械学会論文集B編, Vol.57, No.540 (1991), pp.2530-2537
(4)	Abe, K., “An improved anisotropy-resolving subgrid-scale model with the aid of a scale-similarity modeling concept”, Int. J. Heat Fluid Flow, Vol.39 (2013), pp.42-52.
(5)	Kawai, S. and Larsson, J. “Dynamic non-equilibrium wall-modeling for large eddy simulation at high Reynolds numbers”, Phys. Fluids, Vol.25, No.1 (2013), 015105.
(6)	梶島岳夫, “Get Immersed!”, ながれ, Vol.37, No.6 (2018), pp.503-506.
(7)	Kajishima, T., “Immersed boundary/solid method for the numerical simulation of particle-laden flows”, Fluid Dynamics Res., Vol.51, No. 5 (2019), 051401.
(8)	谷京晨, 竹内伸太郎, 梶島岳夫，“有限サイズの粒子を含む混相流中の渦構造と熱輸送の特徴”, 伝熱, Vol.58, No.242, (2019), pp.16-21.
(9)	岡林希依, 稲岡拓也, 羅文暘, 梶島岳夫, “低迎角における翼周りのキャビテーション乱流の非定常解析”, 日本機械学会論文集, Vol.85, No.876 (2019), 19-00124.
(10)	Fukada, T., Takeuchi, S. and Kajishima, T., “Interaction force and residual stress models for volume-averaged momentum equation for flow laden with particles of comparable diameter to computational grid width”, Int. J. Multiphase Flow, Vol.85 (2016), pp.298-313.
(11)	Fukada, T., Fornari, W., Brandt, L., Takeuchi, S. and Kajishima, T., “A numerical approach for particle-vortex interactions based on volume-averaged equations”, Int. J. Multiphase Flow, Vol.104 (2018), pp.188-205.
(12)	Wang, J.-X., Wu, J.-L. and Xiao, H., “Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data”, Rhys. Rev. Fluids, Vol.2 (2017), 034603.
(13)	Beck, A., Flad, D., Munz, C.-D., “Deep neural networks for data-driven LES closure models”, J. Comput. Phys., Vol.398 (2019), 108910.