流れ　2020年12月号　目次

―　特集テーマ：2020年度年次大会　― 巻頭言 （本澤，森） 乱流のLarge Eddy Simulation の課題 梶島 岳夫（大阪大学） ターボ機械内部流の非定常性について（現象理解と空力・伝熱設計への展開） 船﨑 健一（岩手大学） 固体高分子形燃料電池におけるガス拡散層内部の蒸発を伴う二相流解析モデルの構築 長山 龍也，境田 悟志，田中 光太郎，金野 満（茨城大学） 粒子追跡法によるナノ空間流速分布計測に向けたナノ粒子挙動の統計力学的解析 田中 美典（慶應義塾大学），花崎 逸雄（東京農工大学），嘉副 裕（慶應義塾大学） 年次大会の備忘録　―ウェブ開催の運営的立場から― 伊藤 靖仁（名古屋大学） 年次大会 流体工学部門OS「流体工学の基礎と応用」開催の経緯 および変遷 （森） 　｜　リンク一覧にもどる　｜

 

固体高分子形燃料電池におけるガス拡散層内部の蒸発を伴う二相流解析モデルの構築

長山 龍也 茨城大学	境田 悟志 茨城大学	田中 光太郎 茨城大学	金野 満 茨城大学

１．はじめに

　日本機械学会2020年度年次大会における研究発表について，光栄にもニュースレターとして我々の研究を紹介させていただく機会をいただきました．この場をお借りして選考委員会および日本機械学会の皆様にお礼申し上げます．

　固体高分子形燃料電池は水素と酸素から電気エネルギーを得るエネルギー変換装置であり，高い効率，クリーンな排気，早い起動性といった特徴から自動車の次世代動力源として注目されています．しかし，その普及のためには高電流密度化を実現し，電池の出力密度を向上させる必要があります．この実現に向け，鍵となるのが微細かつ複雑な電池内部の水および蒸気輸送です．

　図1に空気極側の固体高分子形燃料電池の構成を示します．空気極の触媒層では水素極から輸送されてきたプロトンと酸素，電子が反応し水が生成します．生成した水は蒸発，凝縮をともないながらサブマイクロスケールの微細多孔質層および数十マイクロスケールの空孔を有するガス拡散層内を輸送され，電池外部へ排出されます．大きなエネルギーを得るため水素と酸素を多量に反応させた場合，多量の水が生成します．この時，電池内部の水や蒸気輸送が十分に行われなければガス拡散層や微細多孔質層で水が滞留します．滞留した水は触媒層への酸素供給を妨げるため，電流密度は電池内の水の滞留により制限されます．よって，電池内部の水や蒸気輸送を最適化する必要があります．固体高分子形燃料電池は非常に微細かつ複雑な構造を有しているため時間および空間分解能を両立させた観察が難しいため，数値解析による水や蒸気輸送を最適化が有効です．

　我々はこれまでに固体高分子形燃料電池のような複雑形状の流体解析に適した格子ボルツマン法に着目して研究を行ってきました．本稿ではガス拡散層における蒸発をともなう水輸送解析手法の概要について紹介します．

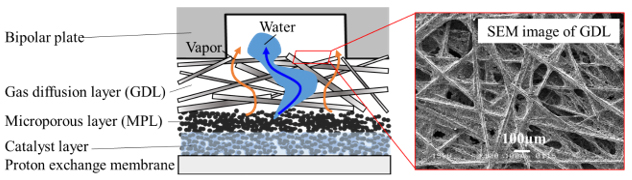
Fig.1 Schematic diagram of polymer electrolyte fuel cell.

２．蒸発を伴う二相流解析モデル

　本研究では固体高分子形燃料電池が対象とする水と空気のような密度比が高い2相流を計算できる稲室らのモデル⁽¹⁾に着目し，次式に示すようにCahn-Hilliard方程式に相変化に関するソース項を加えました．

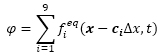(1)

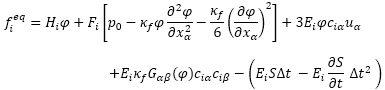(2)

ここでφは秩序変数であり，閾値φ_Lより大きい場合は水として扱い，閾値φ_Gより小さい場合は空気として扱います．f_i^eqは局所平衡分布関数であり，局所平衡分布関数を求める式（2）の最後の項がソース項です．ソース項Sは水および空気でS = 0とし，気液界面において，Sを与えることで蒸発による水の減少を表現します．なお，その他の記号については参考文献1をご参照ください．

　また，蒸発により生成した蒸気の輸送を計算するため，次式の移流拡散方程式も追加しました．

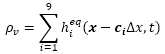(3)

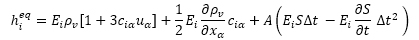(4)

ここでρ_νは蒸気濃度であり，h_i^eqは局所平衡分布関数です．ソース項には秩序変数φを蒸気量ρ_νに変換する定数Aを掛けています．

３．多孔質における解析モデルの検証

　ガス拡散層のような複雑な多孔質構造において蒸発を伴う水の流動を解析できるか検証するために，不均一な細孔を有するガス拡散層を模擬したステンレス製の2次元模型（図2 (a)）を用いて実験と計算結果を比較しました．触媒層で生成した水が微細多孔質層に生じたクラック通してガス拡散層へ流入することを想定し，2次元模型の下部から水を流入させました．一般に多孔質内部の水挙動はキャピラリー数（Ca）で整理されます⁽²⁾．そこで，水の流入速度は固体高分子形燃料電池におけるキャピラリー数であるCa ~ 10^-7となるように調整しています．多孔質の上部には相対湿度0%に保つため乾燥空気を1m/sで流しました．実験は固体高分子形燃料電池の動作温度である70℃に保った恒温槽の中で行い，蒸発をともなう水の流動をCCDカメラで観察しました．図3に実験と解析の比較を示します．各時間において多孔質内の水の分布は実験と解析でおおむね一致していることがわかります．各時間におけるSaturation（s）を比較した結果を図4に示します．ここでSaturationとは多孔質の空孔の割合が水で占められているか示す指標であり，本研究では観察画像から取得した2次元多孔質中の水の面積A_wと空孔面積A_sを用いてs = A_w/ A_sで求めました．結果は実験と解析でよく一致していることから，精度良く蒸発の計算ができていることがわかります．

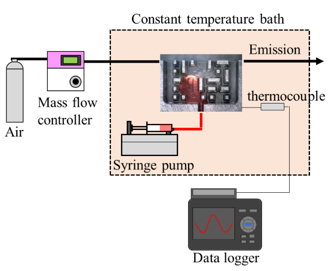(a) Porous area imitating GDL	(b) Overall view of the experimental equipment
Fig.2 Porous area imitating GDL.

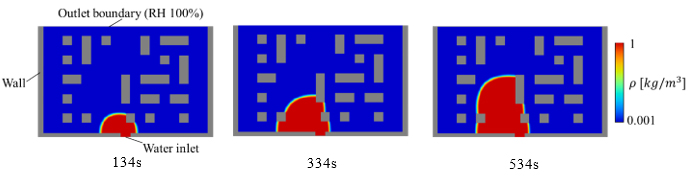
(a) Simulation

(b) Experiment
Fig.3 Comparison of water flow in a two-dimensional porous structure

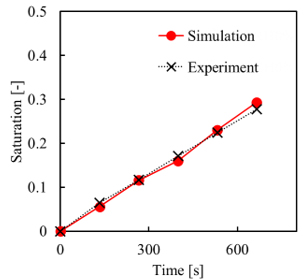
Fig.4 Saturation of complex water flow in porous area

４．おわりに

　固体高分子形燃料電池のガス拡散層を対象として格子ボルツマン法を用いた蒸発を伴う水輸送解析モデルの構築に取り組みました．水と空気のような密度比が高い二相流を計算できる稲室らのモデルに対し，Cahn-Hilliard方程式に相変化に関するソース項を加えるとともに，蒸気に関する移流拡散方程式を導入することで，固体高分子形燃料電池の様な複雑な形状内部での水および蒸気輸送を精度良く解析できることを示しました．構築したモデルを用いて固体高分子形燃料電池の高電流密度化に繋げていきたいと思います．

文献

(1)	稲室隆二，吉野正人，鈴木康裕，格子ボルツマン法入門，丸善出版，(2020).
(2)	Lenormand R, Touboul E, Zarcone C. Numerical models and experiments on immiscible displacements in porous media. J. Fluid Mech., Vol.189, (1988), pp.165-187.