流れ　2020年12月号　目次

―　特集テーマ：2020年度年次大会　― 巻頭言 （本澤，森） 乱流のLarge Eddy Simulation の課題 梶島 岳夫（大阪大学） ターボ機械内部流の非定常性について（現象理解と空力・伝熱設計への展開） 船﨑 健一（岩手大学） 固体高分子形燃料電池におけるガス拡散層内部の蒸発を伴う二相流解析モデルの構築 長山 龍也，境田 悟志，田中 光太郎，金野 満（茨城大学） 粒子追跡法によるナノ空間流速分布計測に向けたナノ粒子挙動の統計力学的解析 田中 美典（慶應義塾大学），花崎 逸雄（東京農工大学），嘉副 裕（慶應義塾大学） 年次大会の備忘録　―ウェブ開催の運営的立場から― 伊藤 靖仁（名古屋大学） 年次大会 流体工学部門OS「流体工学の基礎と応用」開催の経緯 および変遷 （森） 　｜　リンク一覧にもどる　｜

 

粒子追跡法によるナノ空間流速分布計測に向けたナノ粒子挙動の統計力学的解析

田中 美典 慶應義塾大学	花崎 逸雄 東京農工大学	嘉副 裕 慶應義塾大学

　様々な機能を微小空間に集積化するマイクロ流体工学が進展し，近年は10-1000 nmのナノ空間を利用するナノ流体工学へと進展している．ナノ空間を利用することで単一分子レベルの物質輸送や分析，これを応用した1細胞プロテオミクス解析などの実現が期待されている．しかし，ナノ空間では比表面積の増大に伴う表面効果により粘度上昇や誘電率低下など流体がバルクとは異なる特性を有することが報告されており⁽¹⁾，ナノ空間の流速分布の理解が重要である．本稿では，ナノ空間の流速分布計測の実現に向けてこれまで取り組んできた極小空間におけるナノ粒子挙動の研究の概要について述べる．

　一般的な流速分布の計測法として，粒子画像流速計(PIV)が挙げられる．PIVでは流れの中にトレーサ粒子を懸濁して2時刻画像を撮像し，粒子の移動量から流速を計測する．微小空間の代表的なPIVとしてマイクロPIV⁽²⁾がある(図1左)．マイクロPIVでは焦点面をある深さ位置に合わせて画像を撮像することによって，特定の深さ位置における流速を計測する．しかし，深さ方向の空間分解能が焦点面の被写界深度と同程度の数μm程度であることから，それより小さいナノ空間に適用することができない．そこで当研究グループでは，非焦点領域の球面収差を利用して粒子位置を特定するデフォーカス・ナノPIV⁽³⁾を開発してきた(図1右)．非焦点領域で撮像した粒子像の干渉縞の半径Rは粒子の焦点面からの距離と線形の関係にある．よって，画像の半径Rを画像解析によって計算することにより，10 nmの空間分解能で粒子の3次元的な位置を特定することができる．

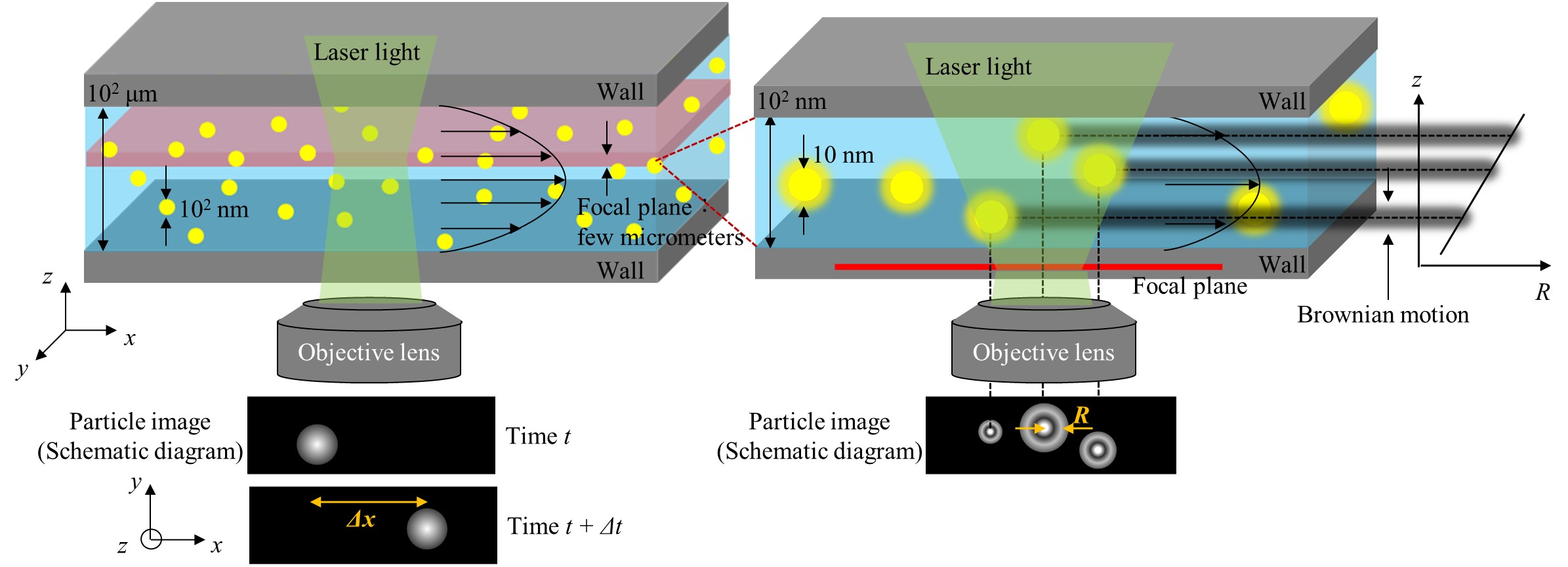
Fig.1  Principle of micro PIV(left) and defocus nano PIV(right)

　しかし，ナノ空間のPIVでは粒子のブラウン運動が大きな誤差要因となり，計測が極めて困難になる．PIVは粒子の移動量を流れによる移動量とみなして計測するが，液体中の粒子は流れに追随するだけでなくブラウン運動によりランダムに振る舞う．従来研究の100 μm空間ではブラウン運動の移動量は無視できるほど小さい．一方，ブラウン運動による粒子の移動量は粒子の直径の平方根に反比例して増大するため，100 nmのナノ空間ではブラウン運動の移動量が空間サイズに比して非常に大きくなる．例えば，直径10 nmの粒子は1秒間に7 μm移動するため，PIV計測においてブラウン運動が非常に大きな誤差要因となる．そのため，ブラウン運動の影響を抑制する計測条件の検討が必要である．

　そこで本研究では，ナノ空間におけるナノ粒子挙動の統計力学的解析を行い， PIV計測におけるブラウン運動の影響を評価し，ブラウン運動の影響を抑制する計測条件を検討した．粒子の挙動はランジュバン方程式によって流れ方向と深さ方向にそれぞれ式(1)，(2)で記述される⁽⁴⁾．ここで，uは流速，D_⊥, D_‖はそれぞれ壁に並行・垂直な方向の粒子の拡散係数，ξは正規分布する乱数である．

(1)

(2)

　ここで，流路深さを400 nm，粒子直径を60 nm，∆tを我々の最近の研究⁽⁵⁾にもとづき2 nsとして，ランジュバン方程式から粒子位置の時間変化を計算した．結果を図2に示す．ブラウン運動によってナノ粒子が深さ方向にランダムに移動していることが見て取れる(図2上部)．ここで，PIVで計測される粒子位置と速度は有限時間での平均となるため，時間分解能が長いほどブラウン運動による誤差が顕在化することが予想される．そこで，異なる時間分解能∆tで得られる粒子速度の分布を求めた(図2下部)．

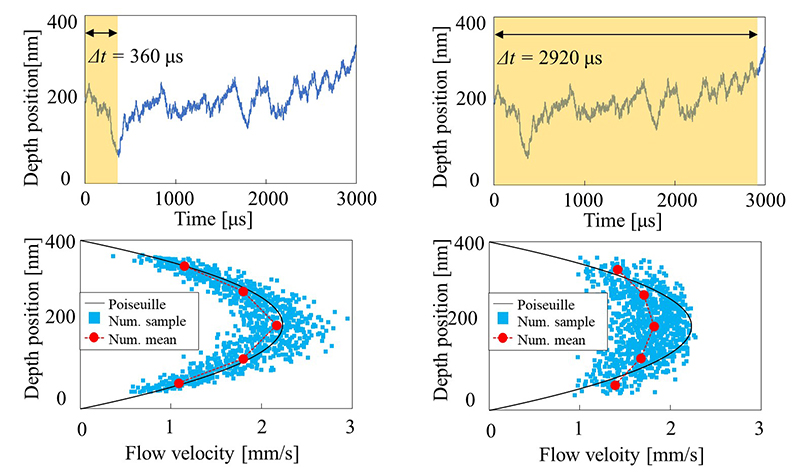
Fig.2  Time variation of particle position in depth-wise direction and
calculation result of velocity distribution of particles: ∆t =360 μs (left) ∆t =2920 μs (right)

　粒子速度はブラウン運動によってばらついているため，流路を深さ方向に5分割し，それぞれの位置で速度の平均値を求めた．比較すると，∆t =360 μsでの平均値の分布はハーゲン・ポアズイユの式から得られる理論値におよそ一致するのに対し， ∆t =2920 μsの分布は大きく平坦化することがわかる．これは∆t 時間中にナノ粒子がブラウン運動により深さ方向にも移動するため，それぞれの深さ位置での速度が平均されたことが原因であると考えられる．以上の統計力学的解析より，本研究で想定したナノ流路の圧力駆動流では，∆t =360 μs以下の計測条件においてブラウン運動を抑制できることが判った．

　これをもとに，実際のナノ流路でデフォーカス・ナノPIVを用いて流速分布を計測した．その結果，統計力学的解析と同様の傾向を示す結果が得られ，∆t =360 μs以下であればブラウン運動による誤差を優位に抑制できることが判った．一方で，ナノ空間特有の流れを示唆する結果も得られている．今後，デフォーカス・ナノPIVの計測システムの開発やさらなる計測条件の検討により，ナノ空間の流速分布計測を実現し，極小空間特有の流動現象を明らかにしていきたい．

　以上，ナノ空間における流速分布計測を目指してこれまで行ってきた研究について述べた．最後に，本発表に際し指導してくださった先生方，ご聴講くださった皆様，本ニュースレター執筆の機会をくださった日本機械学会関係者の皆様に心よりお礼申し上げます．

文献

(1)	Mawatari, K., Tsukahara, T., Sugii, Y., and Kitamori, T., “Extended-nano fluidic systems for analytical and chemical technologies” Nanoscale, 2010. 2(9): pp. 1588-1595.
(2)	Santiago, J.G, Wereley, S.T, Meinhart, C.D, Beebe, D.J, Adrian, R.J, “A particle image velocimetry system for microfluidics” Experiments in Fluids, 1998. 25(4): pp. 316-319.
(3)	Shibata, K., Kazoe, Y., Mawatari, K., and Kitamori, T., “Defocusing nano particle image velocimetry for nanochannel flows”, Proceedings of MicroTAS2017, 2017: pp. 261-262.
(4)	Ermak, D.L. and McCammon, J.A. “Brownian Dynamics with Hydrodynamic Interactions”, Journal of Chemical Physics, 1978. 69(4): pp. 1352-1360.
(5)	Hanasaki, I., Kazoe, Y., and Kitamori, T., “Time resolution effect on the apparent particle dynamics confined in a nanochannel evaluated by the single particle tracking subject to Brownian motion”, Microfluidics and Nanofluidics, 2018. 22(5), 56.