流れ　2021年11月号　目次

―　特集テーマ：2021年度年次大会　― 巻頭言 （本澤，森） 粘弾性流体の乱流－実用例から乱流組織構造まで 川口 靖夫（東京理科大学） 流体解析における計測とシミュレーションの融合とその応用 早瀬 敏幸（東北大学） EFDワークショップ　－流体音－ について 世話人　飯尾 昭一郎（信州大学），渕脇 正樹（九州工業大学），稲澤 歩（東京都立大学），菊地 聡（岐阜大学） 低騒音音響風洞で計測できない空力音 丸田 芳幸（中央大学） 拡張型固有直交展開法を活用した空力音解析 寺島 修，西川 礼恩（富山県立大学），奥野 未侑（金沢大学） ファンの騒音特性とその制御 林 秀千人（長崎大学） 　｜　リンク一覧にもどる　｜

 

流体解析における計測とシミュレーションの融合とその応用

早瀬 敏幸 東北大学

　１．緒言

　流れは，大気や海洋などの地球規模の流れから，流体機器内の流れ，生体内の血流など，幅広い分野の問題に関わっている．特に，気象予測，流れのフィードバック制御，高度医療，原子力プラントの異常同定などにおいては，流れの実現象の正確かつ詳細な状態をできる限り速やかに知る必要があるが，計測や数値シミュレーション単独では，実現象の流れ場を正確に再現することは難しい(Fig. 1)．この問題を，両手法の融合により解決しようとする研究が様々な分野で行われている．気象の数値予測に用いられる4次元同化法，逆問題解析に用いられるティホノフ正則化手法，PIV計測と流れの連続式の融合手法，オブザーバやカルマンフィルタの流れ解析への応用などがある⁽¹⁾．著者等は，オブザーバにおける数学モデルに流れの数値シミュレーションモデルを用いた流れの計測融合シミュレーション(Measurement-integrated simulation， MIシミュレーション)を提案し，様々な流れ場に応用している．MIシミュレーションに関しては，これまでいくつかの解説がある^(2)-(3)．

　本稿では，MIシミュレーションについて，最初に，MIシミュレーションの一般的な定式化について述べた後，MIシミュレーションの応用例として，風洞実験と流体解析を融合したハイブリッド風洞による角柱後流のカルマン渦列を伴う流れ場のリアルタイム解析と，2次元超音波計測融合血流解析システムによる頸動脈血流場の解析について述べる．

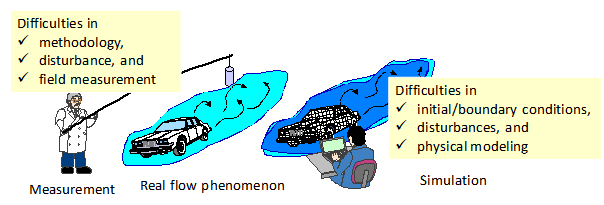
Fig. 1 Measurement and simulation of real-world flow

２．計測融合シミュレーション

　本稿で対象とする計測融合(MI)シミュレーションは，制御理論分野におけるオブザーバの一種である．オブザーバの基本的な構成をFig. 2に示す．オブザーバは，対象とする実現象（プラント）の一部の状態量の計測出力と，計算機上に構成した実現象の数学モデルから，実現象の全ての状態量を取得するものである．実現象と同じ入力を数学モデルに与えて計算を行い，計算で得られた出力信号を計測出力信号と比較する．一般に実現象とは異なる初期値を用いて計算したモデルの出力信号は実際の出力とは異なるので，その誤差に比例したフィードバック信号を数学モデルに加える．フィードバック則が適切に設計されている場合には，出力信号の誤差は時間とともに減少する．さらにシステムが線形で可観測性の条件を満足する場合には，出力誤差の減少に伴い数学モデル内部の全ての状態変数が対応する実システムの値に収束することが保証されている．なお，数値計算の離散化誤差や境界条件の誤差の影響は，出力信号の定常的な誤差として表れるため，逆にこの信号から，離散化手法や境界条件の誤差を評価することも可能である．

 

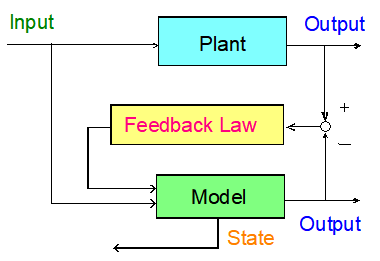
Fig. 2 Structure of observer

2.1 MIシミュレーションの基礎式
　以下に，MIシミュレーションの基礎式について述べる．非圧縮粘性流体を解析対象とすると，その力学的な挙動は，Navier-Stokes式，連続式，および初期条件，境界条件によって支配される．MIシミュレーションでは，実現象と数値シミュレーションの出力の関数として表される外力項を数値シミュレーションに入力する．特に速度と圧力の計測出力と計算出力の線形関数として外力項が表される場合を考える(線形出力フィードバック)．以上がMIシミュレーションの基礎式であり，通常の数値解析アルゴリズムの外力項を計測データと計算結果に基づいて定義することにより，比較的容易に実装が可能である．

2.3 MIシミュレーションの設計
　MIシミュレーションの設計において，本手法は非線形の離散化ナビエ・ストークス方程式と圧力方程式を基礎式としており，通常のオブザーバ理論を直接適用することは困難である．最近では，線形化誤差ダイナミクスに基づく理論的な設計法の研究も行なわれているが，現状では適用は単純な問題に限られる．従って，現状のMIシミュレーションの設計は，物理的な考察に基づき試行錯誤的な方法で行なわれている．

2.4 MIシミュレーションの不安定化現象
　MIシミュレーション設計の問題点として，フィードバックゲインがある臨界値を越えると，誤差が急激に増加する不安定化現象がある．この現象は，流れ場の数値計算における反復計算に伴う解の収束性の問題であることが明らかにされている⁽⁴⁾．フィードバック項を生成項に含めた従来の定式化における安定の十分条件によれば，フィードバックの効果を得るため大きなフィードバックゲインを用いるには，計算時間刻みを小さくする必要がある．本不安定化現象は，反復計算の過程でフィードバック項を未知数に組み込むことにより，回避できることが明らかにされている．

3.　計測融合シミュレーションの例

　MIシミュレーションによる解析例として，一様流中に置かれた角柱後流のカルマン渦列⁽⁹⁾と頸動脈内の血流解析ついて述べる．以下の例における数値解析手法は，全て，等間隔の直角スタガード格子系を用い，有限体積法に基づいて離散化された基礎方程式群を，SIMPLER法に類似の手法で解いたものである⁽⁵⁾．対流項の離散化には物理的考察に基づき再定式化されたQUICKスキームを用いた⁽⁶⁾．また，時間微分項の離散化には2次精度の陰解法を用いた．

3.2. ハイブリッド風洞
　MIシミュレーションを用いて実際に流れの実現象を再現した例として，風洞内の角柱後流のカルマン渦列を解析した結果について述べる⁽⁷⁾．Fig. 3に実験の様子を示す．この例では，風洞実験装置で角柱の後流に生じるカルマン渦列に対して，角柱のよどみ点圧力を基準とした角柱両側面の圧力を計測し，対応する数値計算結果との誤差に比例した仮想力を流れ方向の運動方程式にフィードバックした．さらに，上流よどみ点圧力により一様流速度を推定し，上流速度境界条件として与えた．実験では，１辺3 cmの角柱を用い，主流速度は0.6 m/sとした．対応するレイノルズ数は1200で，実験では不規則な振幅の変動を伴うカルマン渦列が観測された．数値計算条件としては，角柱の１辺に３点の格子点を持つような粗い等間隔格子を用いている．これは，MIシミュレーションにおいて，リアルタイム解析を実現するための計算の高速化を考慮したことと，フィードバックによる精度向上を期待したことによる．

　本MIシミュレーション手法によれば，角柱後流の広い範囲にわたって，カルマン渦列を伴う実際の流れ場の構造が再現できることが示されている．一例として，流脈線の比較をFig. 4に示す．リアルタイム計算を行うためにかなり粗い格子を用いているにもかかわらず，MIシミュレーションでは，カルマン渦による流れの振動の位相も含め，実際の流れ場を正確に再現していることが分かる．なお通常の数値シミュレーションでは，渦の発生が実験に比べてかなり下流側に移動するなど，流れ場の構造を正確に再現できないことが確認されている．

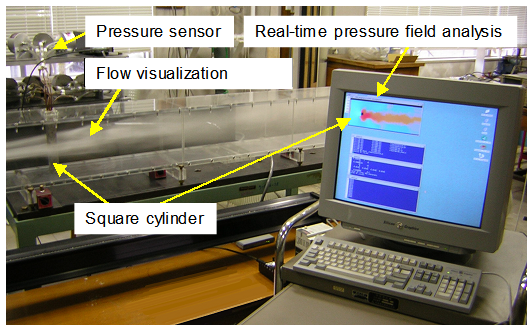
Fig. 3 Real-time analysis of Karman vortices with a hybrid wind tunnel

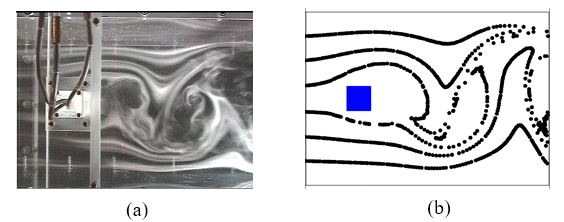
Fig. 4 Streak lines obtained with (a) experiment and (b) MI simulation

3.3. 超音波計測融合シミュレーション
　MIシミュレーションの医療応用として，超音波計測と数値シミュレーションの融合手法による2次元超音波計測融合血流解析システム(Fig. 5)による頸動脈の血流解析について述べる^(8)-(9)．本システムでは，超音波診断装置により血管軸に沿う血管断面形状と超音波ビーム方向の血流速度（ドプラ速度）の時空間分布を測定する．得られた血管形状から計算格子を生成するとともに，ドプラ速度をフィードバックしながらMIシミュレーションを行う．
2次元超音波計測融合血流解析システムにより，頸動脈の血流を解析した例をFig. 6に示す．Fig. 6 (a)は，フィードバックを行わない通常のシミュレーション結果であり，血管形状がほぼストレートであるため，放物分布の速度分布を持つ血流場が得られている．一方，UMIシミュレーション結果のFig. 6 (b)では，ドプラ速度をフィードバックした効果により，複雑な速度分布を持つ血流場が再現されている．ドプラ速度の測定値と計算値を比較することにより，UMIシミュレーションでは通常のシミュレーションに比べてドプラ速度の誤差が1/3程度に減少した．以上より，UMIシミュレーションにより，複雑な血流場が精度よく再現できることが示された．

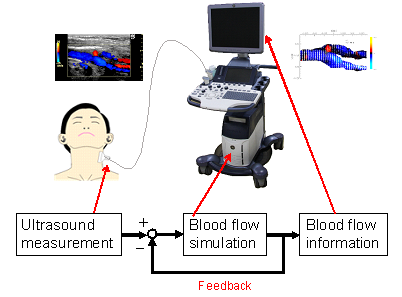
Fig. 5 Two-dimensional ultrasonic-measurement-integrated (UMI) blood flow analysis system

Fig. 6 Analysis results of blood flow in a carotid artery with (a) ordinary simulation and (b) UMI simulation

４．結言

　本稿では，流体解析における計測とシミュレーションの融合手法であるMIシミュレーションについて述べた．最初に，MIシミュレーションの一般的な定式化について述べた後，MIシミュレーションの応用例として，ハイブリッド風洞による角柱後流に発生するカルマン渦列のリアルタイム解析と2次元超音波計測融合血流解析システムによる頸動脈の血流解析について述べた．

参考文献

(1)	Hayase, T., Numerical simulation of real-world flows, Fluid Dynamics Research, Vol. 47, No. 5 (2015) 1-19.
(2)	Hayase, T. A Review of Measurement-Integrated Simulation of Complex Real Flows. J. Flow Control Meas. Visualization 03, 51-66, doi:10.4236/jfcmv.2015.32006 (2015).
(3)	早瀬, 計測融合シミュレーションによる実現象の流れ解析, ターボ機械, 47巻, 9号 (2019) 537-545.
(4)	Nisugi, K.,  Hayase, T., Shirai, A.,  Fundamental Study of Hybrid Wind Tunnel Integrating Numerical Simulation and Experiment in Analysis of Flow Field, JSME International Journal, Ser. B,Vol. 47 (2004), 593-604.
(5)	Hayase, T.・他3名, Stabilization of Measurement-Integrated Simulation by Elucidation of Destabilizing Mechanism, Journal of Fluid Science and Technology, Vol. 5, (2010) 632-647.
(6)	Patankar, S. V., Numerical Heat Transfer and Fluid Flow, 1980, Hemisphere, Washington, DC/New York.
(7)	Hayase, T., Humphrey, J. A. C., Greif, R., A Consistently Formulated QUICK Scheme for Fast and Stable Convergence Using Finite-Volume Iterative Calculation Procedures, Journal of Computational Physics, Vol. 98 (1992), 108-118.
(8)	Funamoto, K., Hayase, T., Shirai, A., Saijo, Y., Yambe, T., Fundamental Study of Ultrasonic-Measurement-Integrated Simulation of Real Blood Flow in the Aorta, Annals of Biomedical Engineering, Vol. 33 (2005), 413-426.
(9)	Kato, T. 他８名, Development and feasibility study of a two-dimensional ultrasonic-measurement-integrated blood flow analysis system for hemodynamics in carotid arteries, Medical & Biological Engineering & Computing, Vol. 52, No. 11 (2014) 933-943.